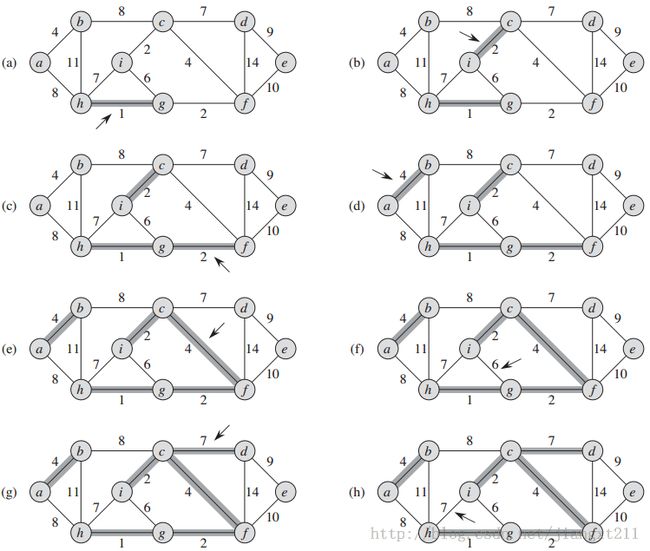
Kruskal算法



在Kruskal算法中，集合A是一个森林，其结点就是给定图的结点。每次加入到集合A中的安全边永远是权重最小的连接两个不同分量的边。在Prim算法中，集合A则是一棵树。每次加入到A中的安全边永远是连接A和A之外某个结点的边中权重最小的边。

 

Kruskal算法找到安全边的办法是，在所有连接森林中两棵不同的树的边里面，找到权重最小的边（u， v）。设C1和C2为边（u， v）所连接的两棵树。由于边（u， v）一定是连接C1和其他某棵树的一条轻量级边，边（u， v）是C1的一条安全边。Kruskal算法属于贪心算法，因为它每次都选择一条权重最小的边加入到森林。

 

Kruskal算法实现

在Kruskal实现过程中，使用一个不相交集合数据结构来维护几个互不相交的元素集合。每个集合代表当前森林中的一棵树。通过FindSet(u)来返回包含元素u集合的代表元素，通过Union来合并两棵树。

#include <stdio.h>
#include <stdlib.h>

#define BUFSIZE 100
#define VERTEXS 10
typedef struct {
	int u;
	int v;
	int weight;
} edge;
edge e[BUFSIZE] = {{'a', 'b', 4}, {'a', 'h', 8}, {'b', 'c', 8},
	{'b', 'h', 11}, {'c', 'd', 7}, {'c', 'f', 4}, {'c', 'i', 2},
	{'d', 'e', 9}, {'d', 'f', 14}, {'e', 'f', 10}, {'f', 'g', 2},
	{'g', 'i', 6}, {'g', 'h', 1}, {'i', 'h', 7}}; // forest

edge A[VERTEXS-1]; // 最小生成树的边集
int parent[VERTEXS]; // 记录前驱
int cost = 0;
	
void MakeSet(int x)
{	
	parent[x] = 0;
}

int FindSet(int x)
{	
	while (parent[x] != 0) // 这里的判断parent[x]的初值有关
		x = parent[x];
	return x;
}
 
bool UnionSet(int x, int y, int w)
{
	if (x != y) { // x, y不相同，将y合并到x中
		parent[y] = x;
		return true;
	}

	return false;
}

void UnionSet(int x, int y)
{
	parent[y] = x;
}

int Compare(const void *a, const void *b)
{	
	return ((edge *)a)->weight - ((edge *)b)->weight;
}

int main()
{
	int n; // 边的个数
//	printf("Please enter the number of edges:");
//	scanf("%d", &n);
//  输入边的信息
// 	for (int i = 0; i < n; i++) {
// 		scanf(("%c %c %d"), &(e[i].u), &(e[i].v), &(e[i].weight));
// 		getchar();
// 		e[i].u -= 'a';
// 		e[i].v -= 'a';
// 	}

	n = 14;
	for (int i = 0; i < BUFSIZE; i++) {
		MakeSet(i);
	}
	// sort the edges of E into nondecreasing order by weight
	int cnt = 0; // A中元素个数（边数）
	qsort(e, n, sizeof(edge), Compare);
	for (int i = 0; i < n; i++) { 
		int x = FindSet(e[i].u);  // 判断u、v是否属于同一棵树
		int y = FindSet(e[i].v);  // 如果是就会形成环
		if (x != y) { 
			A[cnt].u = e[i].u;
			A[cnt].v = e[i].v;
			A[cnt++].weight = e[i].weight;
			UnionSet(e[i].u, e[i].v); // 将y合并到x中
			printf("%c---%c:%d\n", e[i].u, e[i].v, e[i].weight);
			cost += e[i].weight;
		}
	}
	printf("Total weight:%d\n", cost);

	system("pause");
	return 0;
}