牛顿法和拟牛顿法

  牛顿法（Newton method）和拟牛顿法（quasi Newton method）是求解无约束最优化问题的常用方法，有收敛速度快的优点。牛顿法是迭代算法，每一步都需求解目标函数的海塞矩阵（Hessian Matrix），计算比较复杂。拟牛顿法通过正定矩阵近似海塞矩阵的逆矩阵或海塞矩阵，简化了这一计算过程。

---

1、牛顿法

1.1、原理

  牛顿法的原理是使用函数 f(x) f ( x ) 的泰勒级数的前面几项来寻找方程 f(y)=0 f ( y ) = 0 的根。
  将函数 f(x) f ( x ) 在 x0 x 0 处展开成泰勒级数:

f(x)=f(x0)+f′(x0)(x−x0)+12f″(x0)(x−x0)+… f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 1 2 f ″ ( x 0 ) ( x − x 0 ) + …

取其线性部分，作为 f(x) f ( x ) 的近似，则可用 f(x0)+f′(x0)(x−x0)=0 f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) = 0 的解来近似 f(x)=0 f ( x ) = 0 的解，其解为 x1=x0−f(x0)f′(x0) x 1 = x 0 − f ( x 0 ) f ′ ( x 0 ) 。
  由于对 f(x) f ( x ) 的近似只是一阶展开，因此 x1 x 1 并非 f(x)=0 f ( x ) = 0 的解，只能说 f(x1) f ( x 1 ) 比 f(x0) f ( x 0 ) 更接近0。于是，考虑迭代求解：

xn+1=xn−f(xn)f′(xn) x n + 1 = x n − f ( x n ) f ′ ( x n )

迭代过程可参考下图：

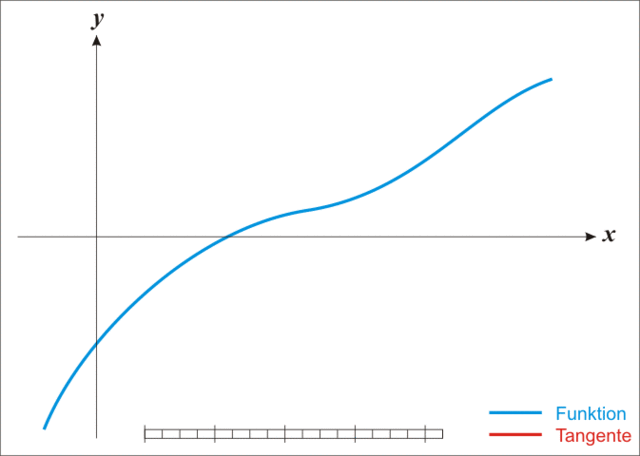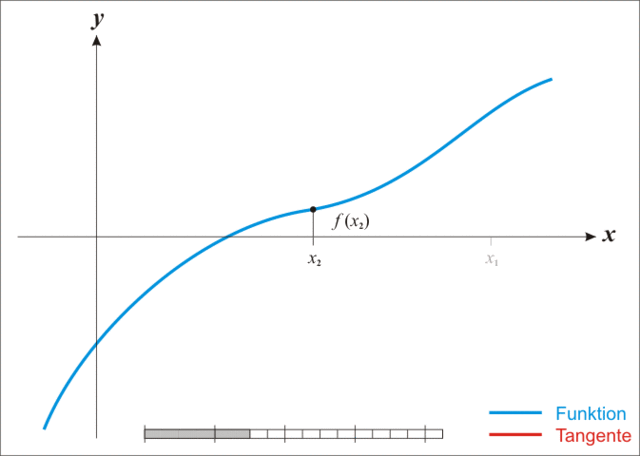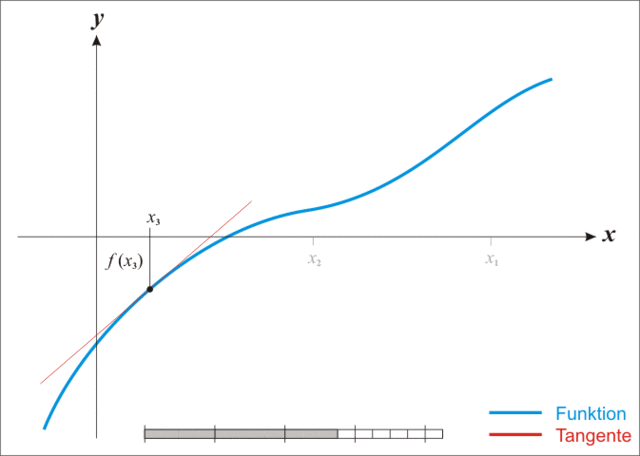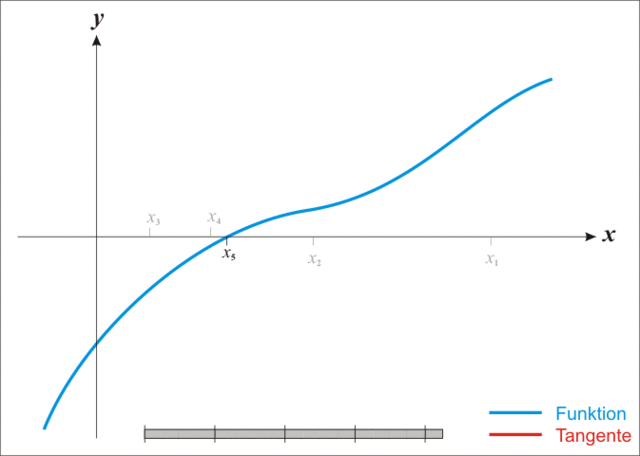
1.2、求解最优化问题

  对于无约束最优化问题 minx∈Rnf(x) min x ∈ R n f ( x ) ，可根据极小点的必要条件 ∇f(x)=0 ∇ f ( x ) = 0 采用牛顿法求解：

xk+1=xk−H−1kgk x k + 1 = x k − H k − 1 g k

其中， gk=g(xk)=∇f(xk) g k = g ( x k ) = ∇ f ( x k ) 是 f(x) f ( x ) 的梯度向量在点 xk x k 的值； Hk=H(xk) H k = H ( x k ) ， H(x)=[∂2f∂xi∂xj]n×n H ( x ) = [ ∂ 2 f ∂ x i ∂ x j ] n × n 是 f(x) f ( x ) 的海塞矩阵。

输入：目标函数 f(x) f ( x ) ，梯度 g(x)=∇f(x) g ( x ) = ∇ f ( x ) ，海塞矩阵 H(x) H ( x ) ，精度要求 ϵ ϵ ；
输出： f(x) f ( x ) 的极小点 x∗ x ∗ 。
（1）取初始点 x0 x 0 ，置 k=0 k = 0
（2）计算 gk g k ，若 ||gk||<ϵ | | g k | | < ϵ ，则 x∗=xk x ∗ = x k ，停止计算；否则转（3）
（3）计算 Hk H k ，令 xk+1=xk−H−1kgk x k + 1 = x k − H k − 1 g k
（4）置 k=k+1 k = k + 1 ，转（2）
注：第（3）步中，涉及到 H−1k H k − 1 的计算，实际应用中，通常并不直接对 Hk H k 进行求逆，而是将其转化为求解线性代数方程组 Hkdk=−gk H k d k = − g k ，此时可根据系数矩阵 Hk H k 的性态来选择合适的迭代法，如预条件共轭梯度法（PCG）、代数多重网格法（AMG）等。

1.3、小结

  当目标函数是二次函数时，海塞矩阵退化成一个常数矩阵，从任一初始点出发，牛顿法可一步到达，因此它是一种具有二次收敛性的算法。对于非二次函数，若函数的二次性态较强，或迭代点已进入极小点的邻域，则其收敛速度也是很快的，这是牛顿法的主要优点。
  牛顿法的迭代公式中由于没有步长因子，是定步长迭代，对于非二次型目标函数，有时会使函数值上升，即出现 f(xk+1)>f(xk) f ( x k + 1 ) > f ( x k ) 的情况，更甚者，可能出现迭代点列 {xk} { x k } 发散而导致计算失败的情况。为解决这个问题，出现了“阻尼牛顿法”，增加一个步长因子 λk λ k ，将算法流程（3）中的计算公式修改为：

xk+1=xk−λkH−1kgk x k + 1 = x k − λ k H k − 1 g k

  牛顿法的另一个弊病在于，每一次迭代都要计算 H−1 H − 1 ，这一步计算比较复杂，下一节的拟牛顿法将解决这个问题。

2、拟牛顿法

  如上节所说，牛顿法虽然收敛速度快，但是需要计算海塞矩阵的逆矩阵 H−1 H − 1 ，而且有时目标函数的海塞矩阵无法保持正定，从而使得牛顿法失效。为了克服这两个问题，人们提出了拟牛顿法。这个方法的基本思想是：不用二阶偏导数而构造出可以近似海塞矩阵（或海塞矩阵的逆）的正定对称阵。不同的构造方法就产生了不同的拟牛顿法。
  下面我们先推导一下拟牛顿条件，它给“对海塞矩阵（或海塞矩阵的逆）做近似”提供了理论指导，指出了用来近似的矩阵应该满足的条件。

2.1、拟牛顿条件

  对 ∇f(x) ∇ f ( x ) 做泰勒展开我们得到了以下近似：

∇f(x)=gk+Hk(x−xk) ∇ f ( x ) = g k + H k ( x − x k )

取 x=xk+1 x = x k + 1 ，即得：

gk+1−gk=Hk(xk+1−xk) g k + 1 − g k = H k ( x k + 1 − x k )

记 yk=gk+1−gk y k = g k + 1 − g k ， δk=xk+1−xk δ k = x k + 1 − x k ，则：

yk=HkδkH−1kyk=δk y k = H k δ k H k − 1 y k = δ k

以上即为拟牛顿条件。
  在拟牛顿法中，选择 Gk G k 作为 H−1k H k − 1 的近似或选择 Bk B k 作为 Hk H k 的近似，并且使得它们满足上述拟牛顿条件即可。

2.2、DFP算法

  DFP算法用 Gk G k 作为 H−1k H k − 1 的近似，这里我们直接给出计算公式：

Gk+1=Gk+δkδTkδTkyk−GkykyTkGkyTkGkyk G k + 1 = G k + δ k δ k T δ k T y k − G k y k y k T G k y k T G k y k

可以证明，如果初始矩阵 G0 G 0 是正定对称的，则迭代过程中的每个矩阵 Gk G k 都是正定对称的，一般取 G0=I G 0 = I 。

2.3、BFGS算法

  BFGS算法用 Bk B k 作为 Hk H k 的近似，与DFP相比，BFGS性能更佳。这里我们直接给出计算公式：

Bk+1=Bk+ykyTkyTkδk−BkδkδTkBkδTkBkδk B k + 1 = B k + y k y k T y k T δ k − B k δ k δ k T B k δ k T B k δ k

可以证明，如果初始矩阵 B0 B 0 是正定对称的，则迭代过程中的每个矩阵 Bk B k 都是正定对称的，一般取 B0=I B 0 = I 。
  若记 Gk=B−1k G k = B k − 1 ， Gk+1=B−1k+1 G k + 1 = B k + 1 − 1 ，那么应用Sherman-Morrison公式可以将上述迭代公式改写为：

Gk+1=(I−δkyTkδTkyk)Gk(I−δkyTkδTkyk)T+δkδTkδTkyk G k + 1 = ( I − δ k y k T δ k T y k ) G k ( I − δ k y k T δ k T y k ) T + δ k δ k T δ k T y k

这就是BFGS算法关于 Gk G k 的迭代公式。

2.4、L-BFGS算法

  在BFGS中，需要用到一个N阶矩阵 Gk G k ，当N很大时，存储这个矩阵将消耗大量计算机资源。为了解决这个问题，减少BFGS迭代过程中所需的内存开销，就有了L-BFGS。
  L-BFGS（Limited-memory BFGS或Limited-storage BFGS）对BFGS进行了近似，其基本思想是：不再存储完整的矩阵 Gk G k ，而是存储计算过程中的向量序列 {δk}{yk} { δ k } { y k } ，需要矩阵 Gk G k 时，利用向量序列 {δk}{yk} { δ k } { y k } 的计算来代替。而且，向量序列 {δk}{yk} { δ k } { y k } 也不是所有的都存储，而是保留最新的m个，每次计算 Gk G k 时，只利用最新的m个向量序列 {δk}{yk} { δ k } { y k } 。这样一来，存储空间由 O(N2) O ( N 2 ) 降至 O(mN) O ( m N ) 。
  具体推导和计算细节，这里不赘述，读者可自行了解。

3、其它

3.1、牛顿法和梯度下降法

  二者都是求解无约束最优化问题的常用方法，牛顿法是二阶收敛，梯度下降法是一阶收敛，所以牛顿法更快，下图形象化地显示了这一点：

其中，红色路径代表牛顿法，绿色路径代表梯度下降法。

3.2、牛顿法和深度学习

  深度学习中，往往采用梯度下降法作为优化算子，而很少采用牛顿法，主要原因有以下几点：

1. 神经网络通常是非凸的，这种情况下，牛顿法的收敛性难以保证；
2. 即使是凸优化，只有在迭代点离全局最优很近时，牛顿法才会体现出收敛快的优势；
3. 可能被鞍点吸引。

---

参考文献

[1] https://www.cnblogs.com/ljy2013/p/5129294.html
[2] https://blog.csdn.net/VictoriaW/article/details/71710280
[3] https://zh.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E6%B3%95
[4] https://www.jiqizhixin.com/articles/2017-03-11-2
[5] https://www.zhihu.com/question/46441403?sort=created
[6] https://baike.baidu.com/item/%E7%89%9B%E9%A1%BF%E6%B3%95/1384129?fr=aladdin
[7] https://www.zhihu.com/question/19723347
[8] https://liuxiaofei.com.cn/blog/lbfgs%E6%96%B9%E6%B3%95%E6%8E%A8%E5%AF%BC/
[9] https://www.cnblogs.com/jiahenhe2/p/8086857.html
[10] https://baike.baidu.com/item/%E6%B3%B0%E5%8B%92%E7%BA%A7%E6%95%B0/7289427?fr=aladdin
以上为本文的全部参考文献，对原作者表示感谢。