pytorch实现MobileNet
论文:https://arxiv.org/pdf/1704.04861.pdf
背景:
为移动端和嵌入式端深度学习应用设计的网络,使得在cpu上也能达到理想的速度要求。2017年4月发布的MobileNet是一个轻量级深度神经网络。
创新点:
主要应用了深度可分离卷积来代替传统的卷积操作,并且放弃pooling层。把标准卷积分解成深度卷积(depthwise convolution)和逐点卷积(pointwise convolution)。这么做的好处是可以大幅度降低参数量和计算量。分解过程示意图如下:
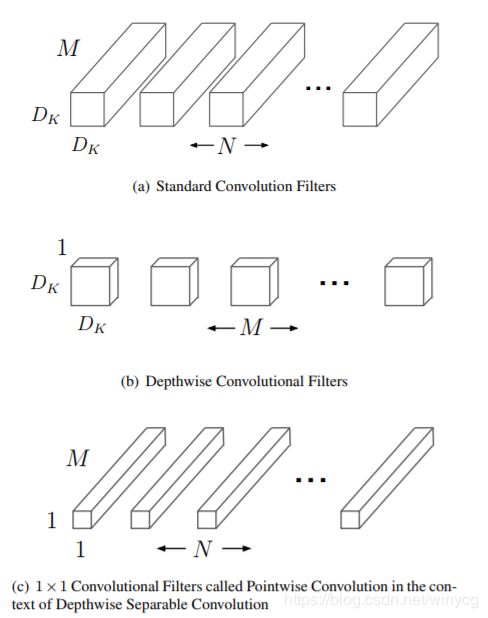
设输入的特征映射为 F F F尺寸为 D F × D F × M D_{F}\times D_{F}\times M DF×DF×M.
标准卷积核 K K K的尺寸为 D K × D K × M × N D_{K}\times D_{K}\times M\times N DK×DK×M×N,则经过标准卷积核处理后,输出的特征维度为: D F × D F × N D_{F}\times D_{F}\times N DF×DF×N,计算量为: N ⋅ D F ⋅ D F ⋅ M ⋅ D K ⋅ D K N\cdot D_{F}\cdot D_{F} \cdot M\cdot D_{K}\cdot D_{K} N⋅DF⋅DF⋅M⋅DK⋅DK
其中,一共 N N N个卷积核,每个卷积核约进行 D F ⋅ D F D_{F}\cdot D_{F} DF⋅DF次扫描,每次扫描的深度(通道数)为 M M M,每一个通道需要进行 D K ⋅ D K D_{K}\cdot D_{K} DK⋅DK次加权求和。
深度卷积的卷积核尺寸为 D K × D K × 1 × M D_{K}\times D_{K}\times1\times M DK×DK×1×M,对特征图处理后的输出维度为: D F × D F × M D_{F}\times D_{F}\times M DF×DF×M
计算量为: M ⋅ D F ⋅ D F ⋅ D K ⋅ D K M\cdot D_{F}\cdot D_{F} \cdot D_{K}\cdot D_{K} M⋅DF⋅DF⋅DK⋅DK
使用逐点卷积对深度卷积处理后的特征图操作,输出维度为: D F × D F × N D_{F}\times D_{F}\times N DF×DF×N,
计算量为: N ⋅ D F ⋅ D F ⋅ M N\cdot D_{F}\cdot D_{F} \cdot M N⋅DF⋅DF⋅M
标准卷积和深度可分离卷积相比,输出的特征图维度相同的,但是计算量的比较为:
M ⋅ D F ⋅ D F ⋅ D K ⋅ D K + N ⋅ D F ⋅ D F ⋅ M N ⋅ D F ⋅ D F ⋅ M ⋅ D K ⋅ D K = 1 N + 1 D K 2 \frac{M\cdot D_{F}\cdot D_{F} \cdot D_{K}\cdot D_{K}+N\cdot D_{F}\cdot D_{F} \cdot M}{N\cdot D_{F}\cdot D_{F} \cdot M\cdot D_{K}\cdot D_{K}}=\frac{1}{N}+\frac{1}{D_{K}^{2}} N⋅DF⋅DF⋅M⋅DK⋅DKM⋅DF⋅DF⋅DK⋅DK+N⋅DF⋅DF⋅M=N1+DK21
当卷积核的尺寸为 3 × 3 3\times 3 3×3时,与标准卷积相比,深度可分离卷积可以减少8-9倍的计算量,仅仅有很小的准确率损失。
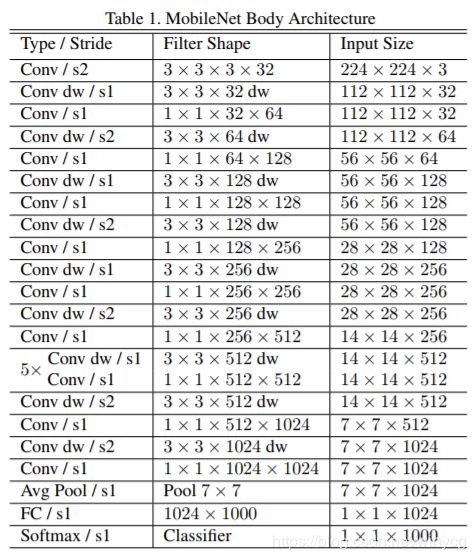
网络结构
卷积层之后对应的BN和ReLU的关系:

除了第一层为标准的卷积层之外,其他的层都为深度可分离卷积。
宽度因子 α \alpha α:
对于深度可分离卷积层,输入的通道数 M M M变为 α M \alpha M αM,输出通道数由 N N N变为 α N \alpha N αN,此时深度可分离卷积层的计算代价变为:
α M ⋅ D F ⋅ D F ⋅ D K ⋅ D K + α N ⋅ D F ⋅ D F ⋅ α M \alpha M\cdot D_{F}\cdot D_{F} \cdot D_{K}\cdot D_{K}+\alpha N\cdot D_{F}\cdot D_{F} \cdot \alpha M αM⋅DF⋅DF⋅DK⋅DK+αN⋅DF⋅DF⋅αM
α ∈ ( 0 , 1 ] \alpha\in (0,1] α∈(0,1],典型的设置为1,0.75,0.5,0.25.
分辨率因子 ρ \rho ρ
对于深度可分离卷积层,输入图像和输出的中间表示的分辨率通过 ρ \rho ρ来改变,,此时深度可分离卷积层的计算代价变为:
α M ⋅ ρ D F ⋅ ρ D F ⋅ D K ⋅ D K + α N ⋅ ρ D F ⋅ ρ D F ⋅ α M \alpha M\cdot \rho D_{F}\cdot \rho D_{F} \cdot D_{K}\cdot D_{K}+\alpha N\cdot \rho D_{F}\cdot \rho D_{F} \cdot \alpha M αM⋅ρDF⋅ρDF⋅DK⋅DK+αN⋅ρDF⋅ρDF⋅αM
ρ ∈ ( 0 , 1 ] \rho\in (0,1] ρ∈(0,1],通过隐式地设置可以使得输入分辨率为224,192,160,128.
通过设置因子可以在资源和准确率之间进行权衡。
import torch
import torch.nn as nn
import torch.nn.functional as F
class Block(nn.Module):
'''Depthwise conv + Pointwise conv'''
def __init__(self, in_planes, out_planes, stride=1):
super(Block, self).__init__()
self.conv1 = nn.Conv2d\
(in_planes, in_planes, kernel_size=3, stride=stride,
padding=1, groups=in_planes, bias=False)
self.bn1 = nn.BatchNorm2d(in_planes)
self.conv2 = nn.Conv2d\
(in_planes, out_planes, kernel_size=1,
stride=1, padding=0, bias=False)
self.bn2 = nn.BatchNorm2d(out_planes)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = F.relu(self.bn2(self.conv2(out)))
return out
class MobileNet(nn.Module):
# (128,2) means conv planes=128, conv stride=2,
# by default conv stride=1
cfg = [64, (128,2), 128, (256,2), 256, (512,2),
512, 512, 512, 512, 512, (1024,2), 1024]
def __init__(self, num_classes=10):
super(MobileNet, self).__init__()
self.conv1 = nn.Conv2d(3, 32, kernel_size=3,
stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(32)
self.layers = self._make_layers(in_planes=32)
self.linear = nn.Linear(1024, num_classes)
def _make_layers(self, in_planes):
layers = []
for x in self.cfg:
out_planes = x if isinstance(x, int) else x[0]
stride = 1 if isinstance(x, int) else x[1]
layers.append(Block(in_planes, out_planes, stride))
in_planes = out_planes
return nn.Sequential(*layers)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.layers(out)
out = F.avg_pool2d(out, 2)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
def test():
net = MobileNet()
x = torch.randn(1,3,32,32)
y = net(x)
print(y.size())
test()