Ceres-Solver学习---(1)

示例：单像空间后方交会

通过上面两个示例大致应该熟悉了Ceres库的使用方式，下面我们编写一个求解摄影测量学里面最基础的一个问题，也就是单张像片的空间后方交会程序。学过《摄影测量学》的人肯定知道，后方交会的求解过程，是非常的麻烦，需要将共线方程求偏导数线性化，然后迭代计算外方位元素。

首先给出共线方程：

式中：x0、y0和f为内方位元素，一般为已知量，abc为旋转矩阵，使用$\phi \omega k$三个角元素来表示为：

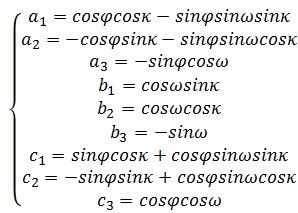
按照教科书上的求解外方位元素的步骤，都需要10步左右，而且中间还需要求改正数迭代计算，非常复杂。这部分内容可以参考下面基本教科书中的内容：

[1]《摄影测量学》张剑清 潘励 王树根武汉大学出版社 P17-P23

[2]《摄影测量学》王佩军 徐亚明 武汉大学出版社 P60-P67

[3]《摄影测量学》林君建 苍桂华 国防工业出版社 P49-P55

下面我们按照Ceres库的方法来编写后方交会的代码，首先编写一个带有模板重载函数()的结构体，用于计算残差。

struct BackCrossResidual
{
  /*
  * X, Y, Z, x, y 分别为观测值，f为焦距
  */
  BackCrossResidual(double X, double Y, double Z, double x, double y, double f)
      :_X(X), _Y(Y), _Z(Z), _x(x), _y(y), _f(f){}
 
  /*
  * pBackCrossParameters：-2分别为Xs、Ys、Zs,3-5分别为Phi、Omega、Kappa
  */
  template 
  bool operator () (const T * const pBackCrossParameters, T* residual) const
  {
      T dXs = pBackCrossParameters[0];
      T dYs = pBackCrossParameters[1];
      T dZs = pBackCrossParameters[2];
      T dPhi = pBackCrossParameters[3];
      T dOmega = pBackCrossParameters[4];
      T dKappa = pBackCrossParameters[5];
 
      T a1  = cos(dPhi)*cos(dKappa) - sin(dPhi)*sin(dOmega)*sin(dKappa);
      T a2  = -cos(dPhi)*sin(dKappa) - sin(dPhi)*sin(dOmega)*cos(dKappa);
      T a3  = -sin(dPhi)*cos(dOmega);
      T b1 = cos(dOmega)*sin(dKappa);
      T b2 = cos(dOmega)*cos(dKappa);
      T b3 = -sin(dOmega);
      T c1 = sin(dPhi)*cos(dKappa) + cos(dPhi)*sin(dOmega)*sin(dKappa);
      T c2 = -sin(dPhi)*sin(dKappa) + cos(dPhi)*sin(dOmega)*cos(dKappa);
      T c3 = cos(dPhi)*cos(dOmega);
 
      // 有两个残差
      residual[0]= T(_x) +T(_f) * T( (a1*(_X-dXs) + b1*(_Y-dYs) + c1*(_Z-dZs)) / ((a3*(_X-dXs) + b3*(_Y-dYs) + c3*(_Z-dZs))));
      residual[1]= T(_y) +T(_f) * T( (a2*(_X-dXs) + b2*(_Y-dYs) + c2*(_Z-dZs)) / ((a3*(_X-dXs) + b3*(_Y-dYs) + c3*(_Z-dZs))));
 
      return true;
  }
 
private:
  const double _X;
  const double _Y;
  const double _Z;
  const double _x;
  const double _y;
  const double _f;
};

对上面的代码解释下，首先有个构造函数，传入的参数共有6个，其中五个是控制点坐标（像方坐标两个xy和物方坐标三个XYZ），另外一个是相机的焦距f。
在重载()函数中，需要的参数初值和残差。初值一共有六个，三个线元素和三个角元素。将三个角元素处理成旋转矩阵所需要的九个参数。

最后按照共线方程编写残差计算公式，这里需要注意的是，一组点可以计算出两个残差，分别是X和Y。

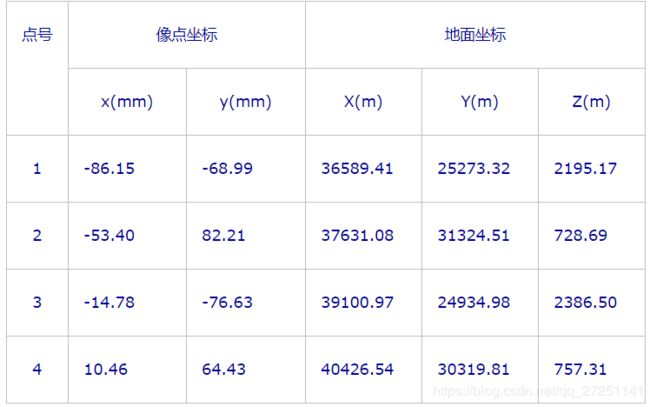
接下来是调用函数，使用的数据是参考书[1]P39第9题（或参考书[2]P89第3题）。题目中给定的相机焦距为153.24mm，坐标点如下表：

int main(int argc, char** argv)
{
  google::InitGoogleLogging(argv[0]);
 
  const char *pszFilename= "C:\\后方交会\\sourcedata.txt";
 
  FILE* fid = fopen(pszFilename,"rt");
  if(!fid)
      return NULL;
 
  int nCount = 4;
  double* pData = new double[5 * nCount];
  memset(pData, 0, sizeof(double)* 5 * nCount);
 
  double dBackCrossParameters[6] = {0};   //初值
  for(int i=0;i(pResidualX), NULL,dBackCrossParameters);
  }
 
  Solver::Options m_options;
  Solver::Summary m_summary;
  m_options.max_num_iterations = 25;
  m_options.linear_solver_type = ceres::DENSE_QR;
  m_options.minimizer_progress_to_stdout = true;
 
  Solve(m_options, &problem,&m_summary);
 
  fprintf(stdout,"Xs=%lfYs=%lf Zs=%lf\n",dBackCrossParameters[0],dBackCrossParameters[1],dBackCrossParameters[2]);
  fprintf(stdout,"Phi=%lfOmega=%lf Kappa=%lf\n",dBackCrossParameters[3],dBackCrossParameters[4],dBackCrossParameters[5]);
  fprintf(stdout,"%s\n",m_summary.FullReport().c_str());
 
  return 0;
}

接下来对上面的代码进行说明，首先读取坐标点对，一共有4对。一对点包含五个值。将所有的点都读到数组pData中。

接下来定义一个数组用来保存未知数和迭代初值。根据后方交会流程，三个角元素的初值在垂直摄影时可以认为其值为0，而对于三个线元素，Xs和Ys初值用所有的控制点的物方横坐标和纵坐标的均值，而Zs根据焦距和摄影比例尺坟墓共同决定。

然后构造一个Problem对象，并将每个控制点作为观测值构造一个误差方程，需要注意的是像平面坐标单位要和物方坐标单位一致，由于像方坐标和焦距都是毫米，所以都要除以1000换算为米。

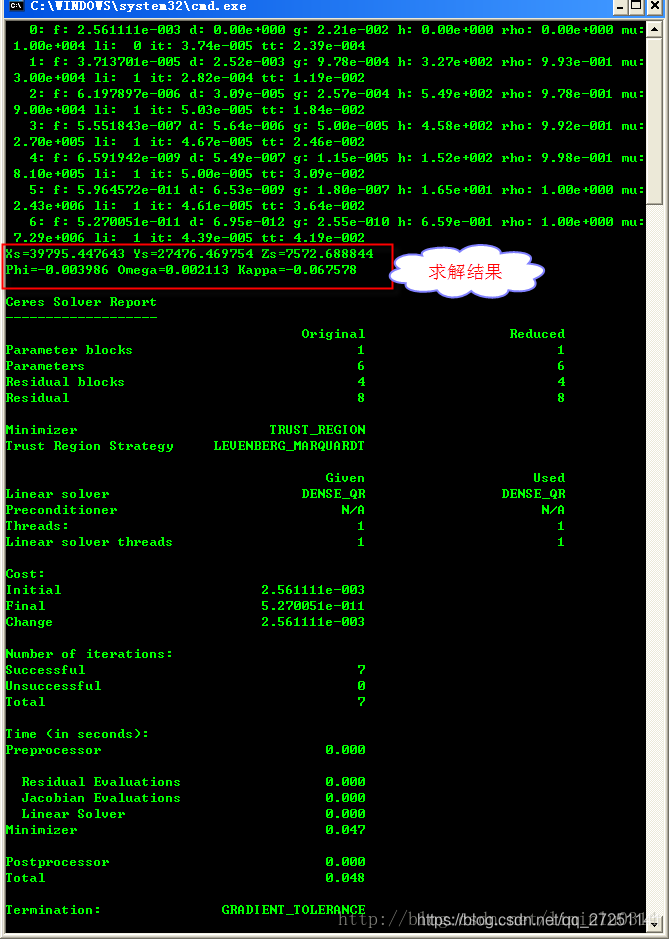
程序执行的结果如下图所示，计算的结果与参考书[1]中给出的参考答案完全一样。此外用我之前用偏导数线性化求解的结果也是一致的，从上面的代码可以看出，使用Ceres库完全可以将很复杂的非线性问题用非常简单的代码来求解。