坐标变换之相机空间之后的事情

3D游戏中的坐标变换一直都是基础中的基础，了解了坐标变换，你就了解了一个3d模型是如何转换到2D屏幕中的。

模型空间->世界空间->相机空间->...->屏幕空间，这篇文章主要是介绍相机空间之后的事情。

先来简单回顾一下模型空间到相机空间的转换，首先世界空间的变换矩阵是由缩放矩阵，旋转矩阵，平移矩阵组成的，缩放和旋转都是线性变换，因此它们可以用一个3乘3的矩阵表示，但是平移矩阵不是线性变换，为了能够把它融入到矩阵乘法中，我们需要使用齐次空间，就是将空间升维到4维空间，因此世界空间的变换矩阵是一个4乘4的矩阵，我们称这个变换为仿射变换。具体细节可以参考我之前写的一篇文章。

相机空间的转换，首先视点是一个点因此对它做缩放变换没有意义。相机空间的变换实际上是把世界空间中的点转换到相机空间中去，因此我只需要获得相机变到到世界空间的逆矩阵，这个矩阵就是相机变化的矩阵。已知相机空间的位置以及相机观察目标的位置，我们可以求出相机的观察方向，这个观察方向就是相机空间的z+轴，然后与世界空间的y+轴进行叉乘，求出右侧的单位向量，然后再叉乘z+轴获得相机空间的y+轴。这样就构建了相机的局部坐标系，通过这个局部坐标系就能够推导出观察矩阵了。

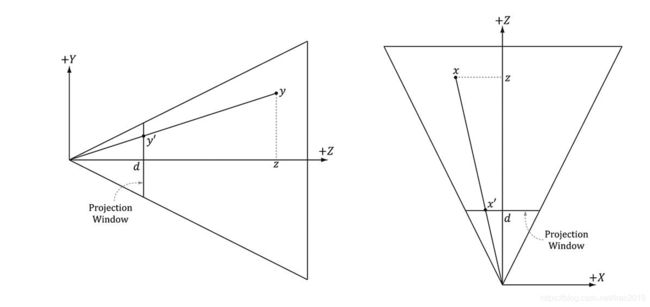
昨天在复习投影矩阵的时候发现龙书中推导投影矩阵，使用的是一个宽度为2，高度为2的投影平面。因为投影平面的宽高是固定的，也就是说视距也是固定的(假定FOV是固定的)，这就是说很有可能近剪切面会在投影平面之前了，赶紧打开unity，看了一下近剪切面的最小值，unity默认最小的近剪切面是0.01(防止除零，后面介绍)，这明显小于视距了，但是渲染效果正常。一头雾水，后来上网查了一下，发现unity使用近剪切面做为投影平面。所以使用近剪切面再次推导了一遍投影矩阵，我靠发现和原先推导出来的结果是一致的，怪不得书里说为了简化推导使用高度为2的投影平面。最后用任意视距d再一次推导，发现结果还是一致的。其实从推导的结果中就可以看出来，投影矩阵跟视距没有关系。推导过程如下：

 

d为视距，r为宽高比，h为高度，w为宽度

同理

将(4)带入到(6)中

把(3)带入(8)

同理

所以

以上就是投影变换公式，接下来思考怎么把这个公式变成矩阵形式，首先可以确定这个公式不是线性变换，怎么证明它不是线性变换我之前的文章有提到过，这里就不再说了。导致这个公式不能做线性变换的原因是这个除数z，如果我们把它先拿出来，做完变换后再除以z，那么剩下的计算过程就可以用矩阵表示了。这就是为什么投影矩阵先把坐标变换到齐次裁剪空间，然后再做透视除法将坐标变换到NDC空间的原因了，透视除法是硬件自己做的，因此我们需要为硬件提供z值，这里的z值应该是相机空间中的z而不是世界空间中的z值。

先来看看这个矩阵

第一个问题，为什么是4*4矩阵，因为之前的变换矩阵都是4*4矩阵，而且我们需要通过w存储z值，为后面的透视除法做准备。

第二个问题，z值怎么没了？为了保证做矩阵乘法，我们把它提取出来了，做完矩阵乘法后再除以z。

第三个问题，这里的A和B是什么鬼?

为了解释上面的问题，首先说一下透视投影的目的：

我们希望将视锥体中的坐标映射到一个叫做NDC的空间，这个空间的取值范围如下：

-1<=x<=1

-1<=y<=1

0<=z<=1

为什么要变换到NDC空间，因为它可以快速的将其转换到屏幕空间，屏幕空间的取值范围是：

0<=x<=1

0<=y<=1

0<=z<=1

NDC空间中的z值直接可以放到深度缓存中了，但是实际上这里还有一个变换就是视口变换我们后面再讲。

在NDC空间之前还有一个齐次裁剪空间，这个空间就是在做透视除法之前的空间，空间的范围取值是:

-w<=x''<=w

-w<=y''<=w

0<=z''<=w

在这个空间图元将会被裁剪，这里的w值其实就是z值。VS输出的顶点就是齐次裁剪空间中的坐标。透视除法这个过程是硬件自己做的，所有我们的投影矩阵要把相机空间的坐标转换到齐次裁剪空间中。为什么，因为透视除法不是线性变换，所以把它拆分成了两步，矩阵乘法只能做到齐次裁剪空间了。

假设相机空间中的坐标是(x,y,z,1)那么乘以上面的透视变换矩阵，坐标就变成了：

这个是齐次裁剪空间下的坐标,经过透视除法变成NDC空间坐标：

看看这个坐标的取值范围是不是NDC坐标系下的取值范围(看推导公式中的9，10)，这一步除以了z，就有了近大远小的效果了。

z在NDC空间中的取值范围是0~1，所以我们只需要根据这个范围，反推出A，B的值就大功告成了。

我们需要构建一个保序函数，这个函数把z坐标从[n,f]映射到[0,1]区间，n和f是远近裁剪面的z值:

根据约束条件我们求解A和B

3带入2得

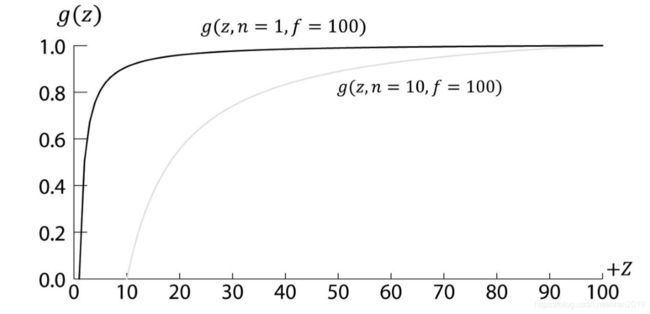
看一下g(z)这个函数得曲线：

可以看到离近剪切面近的区间获得的z值越多，越远获得的z值越少，如果远近裁剪面间的距离越小，z值区间分配越平均。得到z值空间小的区间容易出现z-fighting。

为什么A,B要放到矩阵中那个位置，为了得到这条曲线，当然你也可以不放到对应的位置，并乘以一些乱起八糟的系数，从而获得另外一条曲线，但是Dx就是按照上面的方式做的。

简单总结一下相机变换之后需要经过齐次裁剪空间然后经过透视除法，最后转换到了NDC空间。

这里有个疑问为什么裁剪不在NDC空间做，一定是有原因的，有大神可以回答一下吗？

NDC空间之后就是映射到屏幕空间了，但是因为视口的存在，所以我们不能简单的进行映射。

视口的定义如下：

	// Update the viewport transform to cover the client area.
	mScreenViewport.TopLeftX = 0;
	mScreenViewport.TopLeftY = 0;
	mScreenViewport.Width    = static_cast(mClientWidth);
	mScreenViewport.Height   = static_cast(mClientHeight);
	mScreenViewport.MinDepth = 0.0f;
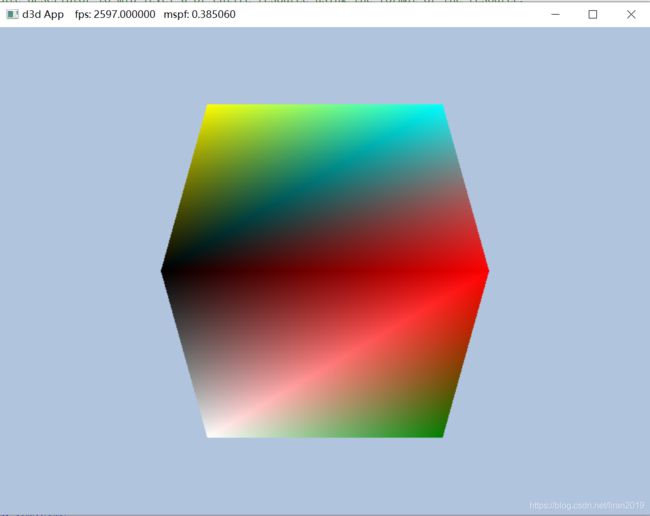
	mScreenViewport.MaxDepth = 1.0f;

如果将视口的宽高设定为窗口的宽高，那么就是我们平时正常看到的效果：

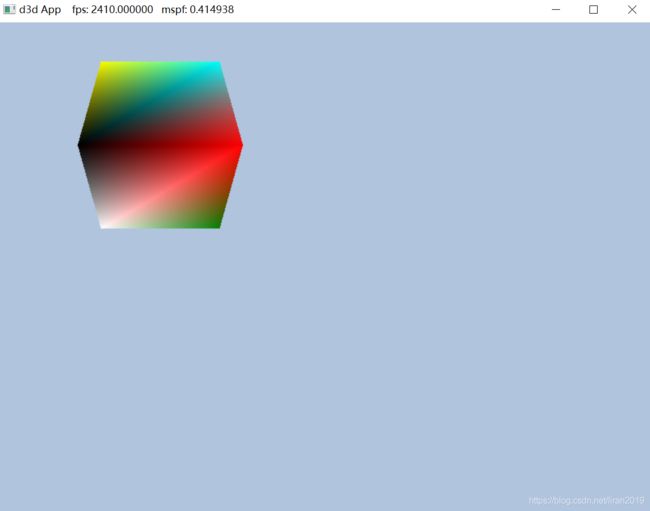
下面的效果是将视口变成原来的4分之一：

这里要注意不是先把场景渲染到后台缓存，然后用视口裁剪，而是把场景映射到视口的小区域中。

mScissorRect = { 0, 0, mClientWidth, mClientHeight };
mCommandList->RSSetScissorRects(1, &mScissorRect);

上面的代码才裁剪区域，效果如下图：

在矩形区域内才会被光栅化。

具体视口矩阵的推导就不写了，贴个链接吧

https://www.cnblogs.com/graphics/archive/2009/10/13/1582773.html