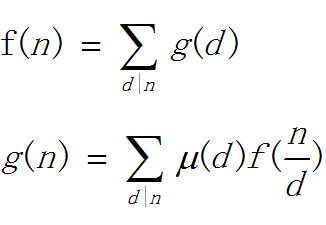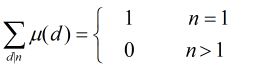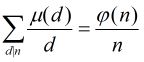莫比乌斯入门（照搬）

神犇博客：https://www.cnblogs.com/linyujun/p/5210772.html

搬这博客是为了自己以后好好系统总结复习。

d|n，表示n能够整除d，也就是d是n的所有因子

 

μ(x)是莫比乌斯函数，它是这样计算的

μ(1) = 1 

x = p1 * p2 * p3 ……*pk（x由k个不同的质数组成）则μ(x) = (-1)^k 

其他情况，μ (x) = 0 

 

证明：https://baike.baidu.com/item/%E8%8E%AB%E6%AF%94%E4%B9%8C%E6%96%AF%E5%8F%8D%E6%BC%94/7348580?fr=aladdin

 

于μ(d)函数，它有如下的常见性质：

    （1）对任意正整数n有

（2）对任意正整数n有 

 

求μ的函数的方法很多

这里提供一种线筛的预处理

#include
const int N = 1e6 + 5;
int mu[N], vis[N], prime[N];
int tot;//用来记录prime的个数
void init(){
    mu[1] = 1;
    for(int i = 2; i < N; i ++){
        if(!vis[i]){
            prime[tot ++] = i;
            mu[i] = -1;
        }
        for(int j = 0; j < tot && i * prime[j] < N; j ++){
            vis[i * prime[j]] = 1;
            if(i % prime[j]) mu[i * prime[j]] = -mu[i];
            else{
                mu[i * prime[j]] = 0;
                break;
            }
        }
    }
}
int main(){
    init();
}

 

其实莫比乌斯有两种描述:

莫比乌斯第一种描述，一般是这种:

莫比乌斯第二种描述，这种也可以而且有些题这种更好:

 

 

题目链接：hdu 1695

此题另一种容斥解法:https://blog.csdn.net/LJD201724114126/article/details/82661566

前面思路一样

先把问题就转化为求1~a区间 和 1~b区间，gcd(x,y) = 1对数的问题

 

设f(d)为满足gcd(x,y)=d的x,y的对数

我们根据莫比乌斯第二描述来做

那F(1) = f(1) + f(2) + f(3) + ....

F(2) = f(2) + f(4) + f(6) +.....

我们可以看出F(d)就是满足gcd(x,y)为d的倍数的x,y的对数

那F(d)的公式就容易求了

F(d) = (a/d) * (b/d)

（在1~a中，有a/d个数是d的倍数，在1~b中，有b/d个数是d的倍数，这些数不管怎么选择，构成的gcd(x,y)都是d的倍数）

因为

 F(1) = f(1) + f(2) + f(3) + ....

所以

f(1) = μ(1)*F(1) + μ(2)*F(2) + μ(3)*F(3) + ...

 

#include
#include
using namespace std;
typedef long long LL;
const int N = 1e6 + 5;
int mu[N], vis[N], prime[N];
int tot;//用来记录prime的个数
void init(){
    mu[1] = 1;
    for(int i = 2; i < N; i ++){
        if(!vis[i]){
            prime[tot ++] = i;
            mu[i] = -1;
        }
        for(int j = 0; j < tot && i * prime[j] < N; j ++){
            vis[i * prime[j]] = 1;
            if(i % prime[j]) mu[i * prime[j]] = -mu[i];
            else{
                mu[i * prime[j]] = 0;
                break;
            }
        }
    }
}
LL Mobius(int a, int b){
    LL ret = 0;
    for(int i = 1; i <= a; i ++){//因为公式中有a/i，所以for到a就可以了 
        ret += 1ll * mu[i] * (a / i) * (b / i);
    }
    //我们现在求完了总对数，但是题目要求的类似(5,7)和(7,5)算一种
    //所以接下来我们开始去重
    LL temp = 0;
    for(int i = 1; i <= a; i ++){
        temp += 1ll * mu[i] * (a / i) * (a / i);
    } 
    return ret - temp / 2;
    //比如a=5,b=7那么(4,6)这样子的区间不可能有重复的(6,4)
    //所以重复的部分只在1~a中，所以最后减去一半的重复区间就好了 
}
int main(){
    init();
    int T, a, b, c, d, k;
    scanf("%d", &T);
    for(int cas = 1; cas <= T; cas ++){
        scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
        if(k == 0){
            printf("Case %d: 0\n", cas);
            continue;
        }
        b /= k; d /= k;
        if(b > d) swap(b, d);
        printf("Case %d: %I64d\n", cas, Mobius(b, d));
    }
}

 

 

这里自己改进了下，删掉重复数时的，但不能AC，样例都过，以后再看

#include
#include
using namespace std;
typedef long long LL;
const int N = 1e6 + 5;
int mu[N], vis[N], prime[N];
int tot;//用来记录prime的个数
void init(){
    mu[1] = 1;
    for(int i = 2; i < N; i ++){
        if(!vis[i]){
            prime[tot ++] = i;
            mu[i] = -1;
        }
        for(int j = 0; j < tot && i * prime[j] < N; j ++){
            vis[i * prime[j]] = 1;
            if(i % prime[j]) mu[i * prime[j]] = -mu[i];
            else{
                mu[i * prime[j]] = 0;
                break;
            }
        }
    }
}
LL Mobius(int a, int b){
    LL ret = 0;
    for(int i = 1; i <= a; i ++){///因为公式中有a/i，所以for到a就可以了
        ret += 1ll * mu[i] * (a / i) * (b / i);
    }
    ///我们现在求完了总对数，但是题目要求的类似(5,7)和(7,5)算一种
    ///所以接下来我们开始去重
    LL temp = 0;
    for(int i = 1; i <= a; i ++){
//            printf("mu[%d]=%d\n",i,mu[i]);
            LL item=(a / i) * (a / i);
        temp += 1ll * mu[i] * ((item-(a/i))/2);
        ///重复的例如1 2 3 4 5，他们的重复数就为 （5*5-5）/2，5*5表示总数，-5表示五个（1,1）（2,2）....
    }

//    printf("ret=%lld.temp=%lld\n",ret,temp);
    return ret - temp ;
    ///比如a=5,b=7那么(4,6)这样子的区间不可能有重复的(6,4)
    ///所以重复的部分只在1~a中，所以最后减去一半的重复区间就好了
}
int main(){
    init();
    int T, a, b, c, d, k;
    scanf("%d", &T);
    for(int cas = 1; cas <= T; cas ++){
        scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
        if(k == 0){
            printf("Case %d: 0\n", cas);
            continue;
        }
        b /= k; d /= k;
        if(b > d) swap(b, d);
        printf("Case %d: %I64d\n", cas, Mobius(b, d));
    }
}
/*
100
1 5 1 7 1
1 5 1 7 0
*/