一.预备知识
积性函数的内容在另外一篇随笔中。
二.重要知识
关于莫比乌斯反演,有很多很好的博客,这里推荐几个
莫比乌斯反演入门 对于这篇博客中的内容,只需要知道 \(\mu\) 其实是一种容斥系数即可,具体的乱七八糟的过程无需理会
莫比乌斯反演简要笔记
(一)莫比乌斯函数
1.莫比乌斯函数 \(\mu(n)\) 的性质
设 \(n=p_{1}^{k_{1}}*p_{2}^{k_{2}}*...*p_{m}^{k_{m}}\),其中 \(p\) 为素数,那么
\[\mu(n)=\begin{cases} 1 \quad\quad\quad\quad n=1 \\\\ (-1)^{m} \quad \prod_{i=1}^{m}k_{i}=1 \\\\ 0 \quad\quad\quad\quad otherwise \end{cases}\]莫比乌斯函数是积性函数,即\(\mu(a)\mu(b)=\mu(a \cdot b)\)
\(\sum_{d|n} \mu(d)=[n=1]\) ,这一点根据二项式定理即可证明
2.线性筛莫比乌斯函数
需要用到的性质
根据 \(\mu\) 的性质可以得到,如果 \(n=p*m\) ,其中 \(p\) 为 \(n\) 的质因子,如果 \(p|m\) 那么显然 \(\mu(n)=0\) ,否则 \(\mu(n)=-\mu(m)\)
miu[1]=1;
For (i,2,n) {
if (!vis[i]) {
p[++N]=i;
miu[i]=-1;
}
For (j,1,N) {
if (i*p[j]>n) break;
vis[i*p[j]]=1;
if (i%p[j]==0) {
miu[i*p[j]]=0;
break;
}
else
miu[i*p[j]]=-miu[i];
}
}(二)莫比乌斯反演
如果 \(f(n)\) , \(g(n)\) 为数论函数,并且满足\[f(n)=\sum_{d|n}g(d)\]
则有莫比乌斯反演\[g(n)=\sum_{d|n}\mu(d)*f(\frac{n}{d})\]
证明在上面的博客中写得很清楚。
但是那个变形式的证明我一直没有弄得很明白,到底如何交换变量?
1.例题一
\(bzoj2190\)
求
\[\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)=k]\]
\[=\sum_{i=1}^{\left\lfloor \frac{n}{k} \right\rfloor}\sum_{j=1}^{\left\lfloor \frac{m}{k} \right\rfloor}[gcd(i,j)=1]\]
因为
\[\sum_{d|n}^{n}\mu(d)=[n=1]\]
所以,可以化为
\[=\sum_{i=1}^{\left\lfloor \frac{n}{k} \right\rfloor}\sum_{j=1}^{\left\lfloor \frac{m}{k} \right\rfloor}\sum_{d|gcd(i,j)}\mu(d)\]
改变枚举量,可以化为
\[\sum_{d=1}^{\left\lfloor\frac{n}{k}\right\rfloor} \mu(d) \left\lfloor\frac{n}{kd}\right\rfloor \left\lfloor\frac{m}{kd}\right\rfloor\]
如果是暴力就是\(O(n)\)的,可以用分块优化到\(\sqrt{n}\)
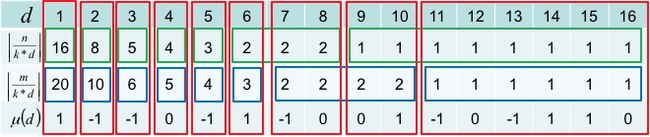
因为有很多取值是连续的,对于相等的段,我们求取\(\mu\)的前缀和,即可批量计算这一个段的答案。
ll solve(int n,int m,int k) {
if (n>m) swap(n,m);
n/=k; m/=k;
ll ans=0;
for (int i=1,nxt=1;i<=n;i=nxt+1) {
nxt=min(n/(n/i),m/(m/i));
ans+=1ll*(sum[nxt]-sum[i-1])*(n/i)*(m/i);
}
return ans;
}2.例题二
求
\[\sum_{i=1}^{n}\sum_{j=1}^{m} gcd(i,j)^k\]
一个重要的方法枚举 \(dx\) 的乘积
\[\sum_{T=1}^{n} \left\lfloor\frac{n}{T}\right\rfloor \left\lfloor\frac{m}{T}\right\rfloor \sum_{d|T}d^{k}\mu(\frac{T}{d})\]
然后设
\[f(T)=\sum_{d|T}d^{k}\mu(\frac{T}{d})\]
再根据积性函数的性质化简即可
具体的过程,上面博客里有,下面对其中的几点做一下说明
- 分块套分块的方法首先是分块\(\left\lfloor \frac{n}{d} \right\rfloor\),因为有很多是一样的,然后再分块 \(\mu\) 后面的那两个
- 后面化简\(f(n)\)的部分因为只有在 \(d\) 取到 \(p_{i}^{x^{i}}\) 或者 \(p_{i}^{x^{i}-1}\) 的时候 \((\frac{T}{d})\) 取到 \(1\) 或者 \(p_{i}\) 的时候 \(\mu\) 值不为0。然后线筛积性函数。
注意,这道题目的解答过程对后面的题目很有帮助,一定要全部弄明白。
他推理的过程中有很多的变量都写错了,但是大体公式还是没问题的。
三.题目
(一)\(bzoj2820\)
求
\[\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j) isprime]\]
分析:
枚举质数
\[=\sum_p\sum_{i=1}^{\left\lfloor \frac{n}{p} \right\rfloor}\sum_{j=1}^{\left\lfloor \frac{m}{p} \right\rfloor}[gcd(i,j)=1]\]
\[=\sum_{p}\sum_{d=1}^{\left\lfloor \frac{n}{p} \right\rfloor}\mu(d)\left\lfloor \frac{n}{pd} \right\rfloor\left\lfloor \frac{m}{pd} \right\rfloor\]
然后枚举乘积\(pd\)
\[=\sum_{T=1}\left\lfloor \frac{n}{T} \right\rfloor \left\lfloor \frac{n}{T} \right\rfloor\sum_{p|T}\mu(\frac{T}{p})\]
但是,如果设
\[f(T)=\sum_{p|T}\mu(\frac{T}{p})\]
\(f(T)\)不是积性函数
所以需要用到一个新的方法,在预处理的时候,枚举质数 \(p\) ,枚举 \(T\) ,然后将 \(p\) 的每一个倍数 \(T\) 都加上 \(\mu(\frac{T}{p})\) ,然后求 \(f(n)\) 就可以做到 \(O(1)\)
再加上前面的分块求 \(T\) ,因此总时间复杂度为 \(O(T\sqrt{n}+maxn)\)
当然,还有一种方法,详情看here
最后再上代码
#include
#include
#include
#include
#include
typedef long long ll;
typedef double dd;
#define For(i,j,k) for (int i=j;i<=k;++i)
#define Forr(i,j,k) for (int i=j;i>=k;--i)
#define Set(a,p) memset(a,p,sizeof(a))
using namespace std;
templatebool chkmax(T &a,T b) { return abool chkmin(T &a,T b) { return a>b?a=b,1:0; }
const int maxn=1e7+1e2;
const int maxx=1e7;
int n,m,N;
int p[maxn],miu[maxn],vis[maxn],sum[maxn],t[maxn];
inline void read(int &x) {
x=0;
int p=1;
char c=getchar();
while (!isdigit(c)) {if (c=='-') p=-1; c=getchar();}
while (isdigit(c)) {x=(x<<1)+(x<<3)+(c-'0'); c=getchar();}
x*=p;
}
inline void init() {
miu[1]=1;
For (i,2,maxx) {
if (!vis[i]) {
p[++N]=i; miu[i]=-1;
}
For (j,1,N) {
if (1ll*i*p[j]>maxx) break;
vis[i*p[j]]=1;
if (i%p[j]==0) {
miu[i*p[j]]=0;
break;
}
else miu[i*p[j]]=-miu[i];
}
}
For (i,1,N) {
for (int j=p[i];j<=maxx;j+=p[i]) t[j]+=miu[j/p[i]];
}
For (i,1,maxx) t[i]=t[i-1]+t[i];
}
int main() {
init();
int tt; read(tt);
while (tt--) {
read(n); read(m);
if (n>m) swap(n,m);
ll ans=0;
for (int i=1,nxt=1;i<=n;i=nxt+1) {
nxt=min(n/(n/i),m/(m/i));
ans+=1ll*(n/i)*(m/i)*(t[nxt]-t[i-1]);
}
printf("%lld\n",ans);
}
return 0;
} (二)\(P3768\)
求
\[\sum_{i=1}^{n}\sum_{j=1}^{n}ijgcd(i,j)\]
\[=\sum_{d=1}^{n}d\sum_{i=1}^{n}\sum_{j=1}^{n}ij[gcd(i,j)=d]\]
\[=\sum_{d=1}^{n}d^3\sum_{i=1}^{\left\lfloor \frac{n}{d} \right\rfloor}\sum_{j=1}^{\left\lfloor \frac{n}{d} \right\rfloor}ij[gcd(i,j)=1]\]
\[=\sum_{d=1}^{n}d^3\sum_{i=1}^{\left\lfloor \frac{n}{d} \right\rfloor}\sum_{j=1}^{\left\lfloor \frac{n}{d} \right\rfloor}ij\sum_{x|gcd(i,j)}\mu(x)\]
\[=\sum_{d=1}^{n}d^3\sum_{x=1}^{\left\lfloor \frac{n}{d} \right\rfloor}\mu(x)x^2\sum_{i=1}^{\left\lfloor \frac{n}{dx} \right\rfloor}\sum_{j=1}^{\left\lfloor \frac{n}{dx} \right\rfloor}ij\]
令\(F(n)=\sum_{i=1}^{n}\sum_{j=1}^{n}ij=\sum_{i=1}^{n}i^3=(\sum_{i=1}^{n})^2\),所以
\[=\sum_{d=1}^{n}d^3\sum_{x=1}^{\left\lfloor \frac{n}{d} \right\rfloor}\mu(x)x^2F(\left\lfloor \frac{n}{dx} \right\rfloor)\]
令\(T=dx\),改变枚举变量(干脆把向下取整去掉,反正程序中是这样的,不然写起来好麻烦)
\[=\sum_{T=1}^{n}\sum_{d|T}d^3\mu(\frac{T}{d})(\frac{T}{d})^2F(\frac{n}{T})\]
\[=\sum_{T=1}^{n}F(\frac{n}{T})T^2\sum_{d|T}d\mu(\frac{T}{d})\]
然后,根据\(\mu\)函数的性质,我们可以得到
\[id*\mu=1*\varphi*\mu=\varepsilon*\varphi=\varphi\]
所以原式可化为
\[=\sum_{T=1}^{n}F(\frac{n}{T})T^2\varphi(T)\]
这看着就清爽多了!前半部分分块处理,后面杜教筛
设\(f(i)=i^2*\varphi(i)\),\(S(n)=\sum_{i=1}^{n}f(i)\)
杜教筛公式:
\[g(1)*S(n)=\sum_{i=1}^{n}(f*g)(i)-\sum_{i=2}^{n}g(i)*S(\frac{n}{i})\]
设\(g(x)=x^2\),那么
\[(f*g)(i)=\sum_{d|i}f(d)*g(\frac{i}{d})=\sum_{d|i}d^2*\varphi(d)*(\frac{i}{d})^2=i^2*\sum_{d|i}\varphi(d)=i^3\]
所以
\[S(n)=\sum_{i=1}^{n}i^3-\sum_{i=2}^{n}i^2*S(\frac{n}{i})\]
再然后,就可以开始打程序了!
当然,事实上是,用 \(\varphi\) 更简单here
\[=\sum_{d=1}^{n}\varphi(d)\sum_{d|i}\sum_{d|j}ij\]
\[=\sum_{d=1}^{n}\varphi(d) d^2 \sum_{i=1}^{\left\lfloor \frac{n}{d} \right\rfloor}i^3\]
我这篇代码被卡常了,对着别人的程序调了好久,但是还是很慢,不知道为什么......
在计算\(sum\)和\(sq\)是时候,\(n\)一进去就要取模!
#include
#include
#include
#include
#include
#include (三)\(bzoj2693\),\(P4313\)
求
\[\sum_{i=1}^{n}\sum_{i=1}^{m}lcm(i,j)\]
ymy大佬的博客中推导过程和我一样的,所以我就懒得写了
\[=\sum\limits_{i=1}^n\sum\limits_{j=1}^m \frac{ij}{gcd(i,j)}\]
\[=\sum\limits_{d=1}^n \frac{1}{d}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m} ij[gcd(i,j)=d] =\sum\limits_{d=1}^n d\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor} ij[gcd(i,j)=1]\]
\[=\sum\limits_{d=1}^n d\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor} ij\sum\limits_{x|gcd(i,j)}\mu(x) =\sum\limits_{d=1}^n d\sum\limits_{x=1}^{\lfloor\frac{n}{d}\rfloor}\mu(x)x^2\sum\limits_{i=1}^{\lfloor\frac{n}{dx}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{dx}\rfloor} ij\]
设\(f(T)=\sum\limits_{i=1}^{\lfloor\frac{n}{T}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{T}\rfloor} ij=\sum\limits_{i=1}^{\lfloor\frac{n}{T}\rfloor}i\sum\limits_{j=1}^{\lfloor\frac{m}{T}\rfloor}j\),所以
\[=\sum\limits_{T=1}^n f(T)\sum\limits_{d|T}\mu(d)*d^2\frac{T}{d} =\sum\limits_{T=1}^n f(T)*T\sum\limits_{d|T}\mu(d)*d\]
设\(g(n)=\sum\limits_{d|n}\mu(d)*d\) ,则\(g\) 为积性函数,可以线筛。
#include
#include
#include
#include
#include
typedef long long ll;
typedef double dd;
#define For(i,j,k) for (int i=j;i<=k;++i)
#define Forr(i,j,k) for (int i=j;i>=k;--i)
#define Set(a,p) memset(a,p,sizeof(a))
using namespace std;
templatebool chkmax(T& a,T b) {return abool chkmin(T& a,T b) {return a>b?a=b,1:0;}
const int maxn=10000000+100;
const int maxx=10000000;
const ll modd=100000009;
int n,m,N;
int vis[maxn],p[maxn];
ll inv;
ll f[maxn],sum[maxn];
inline void read(int &x) {
x=0;
int p=1;
char c=getchar();
while (!isdigit(c)) {if (c=='-') p=-1; c=getchar();}
while (isdigit(c)) {x=(x<<1)+(x<<3)+(c-'0'); c=getchar();}
x*=p;
}
inline void init() {
f[1]=1;
For (i,2,maxx) {
if (!vis[i]) {
p[++N]=i; f[i]=1-i;
}
For (j,1,N) {
int k=i*p[j];
if (k>maxx) break;
vis[k]=1;
if (i%p[j]==0) {
f[k]=f[i]; break;
}
else f[k]=f[i]*(1-p[j])%modd;
}
}
For (i,1,maxx) f[i]=(f[i-1]+f[i]*i%modd+modd)%modd;
For (i,1,maxx) {
sum[i]=sum[i-1]+i;
if (sum[i]>modd) sum[i]-=modd;
}
}
int main() {
init();
int tt; read(tt);
while (tt--) {
ll ans=0;
read(n); read(m);
if (n>m) swap(n,m);
for (int i=1,nxt;i<=n;i=nxt+1) {
nxt=min(n/(n/i),m/(m/i));
ans+=sum[n/i]*sum[m/i]%modd*(f[nxt]-f[i-1])%modd;
ans%=modd;
}
printf("%lld\n",(ans+modd)%modd);
}
return 0;
} (四)\(bzoj3994\)
设 \(d(n)\) 为 \(n\) 的约数个数,求
\[\sum_{i=1}^{n}\sum_{j=1}^{m}d(ij)\]
分析:
\[=\sum_{i=1}^{n}\sum_{j=1}^{m}\sum_{p|i}\sum_{q|j}[gcd(p,q)=1]\]
\[=\sum_{p=1}^{n}\sum_{q=1}^{m}\left\lfloor \frac{n}{p} \right\rfloor \left\lfloor \frac{m}{q} \right\rfloor[gcd(p,q)=1]\]
\[=\sum_{i=1}^{n}\sum_{j=1}^{m}\left\lfloor \frac{n}{i} \right\rfloor \left\lfloor \frac{m}{j} \right\rfloor[gcd(i,j)=1]\]
\[=\sum_{d=1}^{n}\mu(d)\sum_{i=1}^{\left\lfloor \frac{n}{d} \right\rfloor}\sum_{j=1}^{\left\lfloor \frac{m}{d} \right\rfloor}\left\lfloor \frac{n}{id} \right\rfloor\left\lfloor \frac{m}{id} \right\rfloor\]
然后,一个智障的变化,我一下子还没想出来
\[=\sum_{d=1}^{n}\mu(d)\sum_{i=1}^{\left\lfloor \frac{n}{d} \right\rfloor}\left\lfloor \frac{n}{id} \right\rfloor\sum_{j=1}^{\left\lfloor \frac{m}{d} \right\rfloor}\left\lfloor \frac{m}{id} \right\rfloor\]
设
\[f(n)=\sum_{i=1}^{n}\left\lfloor \frac{n}{i} \right\rfloor\]
这个显然可以分块,然后就可以化为
\[=\sum_{d=1}^{n}\mu(d)f(\left\lfloor \frac{n}{d} \right\rfloor)f(\left\lfloor \frac{m}{d} \right\rfloor)\]
后面的在 \(O(n\sqrt{n})\) 预处理之后可以 \(O(1)\) 计算,前面的分块 \(O(\sqrt{n})\)
总时间复杂度 \(O(n\sqrt{n}+T\sqrt{n})\)
#include
#include
#include
#include
#include
typedef long long ll;
typedef double dd;
#define For(i,j,k) for (register int i=j;i<=k;++i)
#define Forr(i,j,k) for (register int i=j;i>=k;--i)
#define Set(a,p) memset(a,p,sizeof(a))
using namespace std;
templatebool chkmax(T &a,T b) { return abool chkmin(T &a,T b) { return a>b?a=b,1:0; }
const int maxn=50000+100;
const int maxx=50000;
int n,m,N;
int p[maxn],vis[maxn],mu[maxn],sum[maxn],s[maxn];
inline void read(int &x) {
x=0;
int p=1;
char c=getchar();
while (!isdigit(c)) {if (c=='-') p=-1; c=getchar();}
while (isdigit(c)) {x=(x<<1)+(x<<3)+(c-'0'); c=getchar();}
x*=p;
}
inline void init() {
mu[1]=1;
For (i,2,maxx) {
if (!vis[i]) {
p[++N]=i; mu[i]=-1;
}
For (j,1,N) {
if (i*p[j]>maxx) break;
int k=i*p[j];
vis[k]=1;
if (i%p[j]==0) {
mu[k]=0; break;
}
else mu[k]=-mu[i];
}
}
For (i,1,maxx) {
sum[i]=sum[i-1]+mu[i];
for (int p=1,nxt=1;p<=i;p=nxt+1) {
nxt=i/(i/p);
s[i]+=(nxt-p+1)*(i/p);
}
}
}
inline void solve() {
if (n>m) swap(n,m);
ll ans=0;
for (int i=1,nxt=1;i<=n;i=nxt+1) {
nxt=min(n/(n/i),m/(m/i));
ans+=1ll*s[n/i]*s[m/i]*(sum[nxt]-sum[i-1]);
}
printf("%lld\n",ans);
}
int main() {
init();
int tt; read(tt);
while (tt--) {
read(n); read(m);
solve();
}
return 0;
}