三维薄板样条,用于三维模型变形(c++)
刚接触变形算法,其实不想碰三维变形算法,菜鸡一个,但是导师一直让试试,那就试试,事实证明薄板样条并不特别适用于古建筑点云变形,第一次写文章只为记录一下我曾经学过,不然按照本人的记忆力,基本都忘完。
薄板样条一般用于图像匹配,二维图像处理无敌,三维真的不是那么太强,起码基本只能二维变形,将三维视为二维,忽略第三维信息,用二维图像提取轮廓,在用相似三角形进行变形,着实凑巧,这里说的是 基于轮廓线与薄板样条的三维自动化建模方法 毕竟论文种可以完全避免同时三个维度的变形,咱也不知道说的对不对。经过这些天的死磕研究,自己写的三维薄板样条的代码总是并不是特别好的变形。简单的圆柱体、长方体、正方体。提供控制点和形变坐标就可以变形,然而使用一些点云的时候,最后通过薄板样条计算出的点各式各样,五花八门。
失败的就不放了,丢人现眼。本来不想碰拉普拉斯的,看来还得去自己编。
static double tps_base_func(double r)//用于计算基函数的r
{
if (r == 0.0)
return 0.0;
else
return r*r * log(r*r);
}
static void calc_tps()
{
// You We need at least 3 points to define a plane
if (control_points.size() < 3)
return;
unsigned p = control_points.size();
// Allocate the matrix and vector
matrix mtx_l(p + 4, p + 4);//L矩阵
matrix mtx_v(p + 4, 3);//包含了v 和 o
matrix mtx_orig_k(p, p);//K矩阵
matrixw(p, 4);
double a = 0.0;
for (unsigned i = 0; i < p; ++i)
{
for (unsigned j = i + 1; j < p; ++j)
{
mtx_l(i, j) = mtx_l(j, i) =
mtx_orig_k(i, j) = mtx_orig_k(j, i) = tps_base_func((control_points[i] - control_points[j]).len()); //tps_base_func(elen);//???//Uij传给上下对角
//a += elen * 2; // same for upper & lower tri
}
}
a /= (double)(p*p);//a=a/p^2
// Fill the rest of L
for (unsigned i = 0; i < p; ++i)
{
// diagonal: reqularization parameters (lambda * a^2)对角线重新量化参数
mtx_l(i, i) = mtx_orig_k(i, i) =
regularization * (a*a);//变形程度 目前为0
// P (p x 3, upper right) 已改 4*P 增加Y
mtx_l(i, p + 0) = 1.0;
mtx_l(i, p + 1) = control_points[i].x;
mtx_l(i, p + 2) = control_points[i].y;
mtx_l(i, p + 3) = control_points[i].z;
//fill P up right and down left
mtx_l(p + 0, i) = 1.0;
mtx_l(p + 1, i) = control_points[i].x;
mtx_l(p + 2, i) = control_points[i].y;
mtx_l(p + 3, i) = control_points[i].z;
}
// O (3 x 3, lower right) 改4*4
for (unsigned i = p; i < p + 4; ++i)
{
for (unsigned j = p; j < p + 4; ++j)
{
mtx_l(i, j) = 0.0;
}
}
// Fill the right hand vector V maybe is matrix
for (unsigned j = 0; j < 3; ++j)
{
for (int i = 0; i < 4; i++)
{
mtx_v(p + i, j) = 0;
}
}
for (size_t i = 0; i < TransformationPoint.size(); i++)
{
mtx_v(i, 0) = TransformationPoint[i].x;
mtx_v(i, 1) = TransformationPoint[i].y;
mtx_v(i, 2) = TransformationPoint[i].z;
}
cout << "--------------------L矩阵-----------------" << endl;
for (unsigned i = 0; i < p+4; i++)
{
for (unsigned j = 0; j < p+4; j++)
{
cout << mtx_l(i, j) << "\t";
}
cout << endl;
}
cout << " ----------------v矩阵-----------------------" << endl;
for (int i = 0; i < p+4; i++)
{
for (int j = 0; j < 3; j++)
{
cout << mtx_v(i, j) << "\t";
}
cout << endl;
}
if (0!= LU_Solve(mtx_l, mtx_v)&&1== LU_Solve(mtx_l, mtx_v))//0为成功 1为奇异矩阵 2 行数不对等
{
puts("Singular matrix! Aborting.");
cout << "计算不成功,奇异矩阵" << endl;
exit(1);
}
cout << "---------------------------系数----------------------------------" << endl;
for (int i = 0; i < p + 4; i++)
{
for (int j = 0; j < 3; j++)
{
cout << mtx_v(i, j) << "\t";
}
cout << endl;
}
//WxU WyU WzU权重分配
float WxU = 0;
float WyU = 0;
float WzU = 0;
for (int i = 0; i < EnteredPoint.size(); i++)
{
double x= mtx_v(p + 0, 0) + mtx_v(p + 1, 0)*EnteredPoint[i].x
+ mtx_v(p + 2, 0)*EnteredPoint[i].y + mtx_v(p + 3, 0)*EnteredPoint[i].z;
double y= mtx_v(p + 0, 1) + mtx_v(p + 1, 1)*EnteredPoint[i].x
+ mtx_v(p + 2, 1)*EnteredPoint[i].y + mtx_v(p + 3, 1)*EnteredPoint[i].z;
double z= mtx_v(p + 0, 2) + mtx_v(p + 1, 2)*EnteredPoint[i].x
+ mtx_v(p + 2, 2)*EnteredPoint[i].y + mtx_v(p + 3, 2)*EnteredPoint[i].z;
for (int j = 0; j < p; j++)//权重系数很小
{
WxU += mtx_v(j, 0) * tps_base_func((EnteredPoint[i] - control_points[j]).len());
WyU += mtx_v(j, 1) * tps_base_func((EnteredPoint[i] - control_points[j]).len());
WzU += mtx_v(j, 2) * tps_base_func((EnteredPoint[i] - control_points[j]).len());
}
//cout <<"v "<< x+WxU << " " << y + WyU << " " << z + WzU << "" << endl;
//cout << WxU << " " << WyU << " " << WzU << endl;
std::cout << "计算第" << i << "次" << " " << "还剩" << EnteredPoint.size() - i << "待计算" << std::endl;
cout <<" v "< be = prod(prod >(trans(w), mtx_orig_k), w);
bending_energy = be(0, 0);
cout << "弯曲能量为= " << bending_energy << endl;
}
void ReadControlPoint()
{
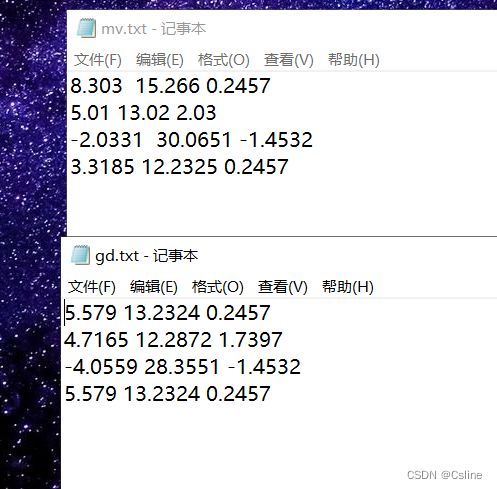
ifstream infile("E:\\ExperimentalData\\expData\\test\\gd.txt");
float a, b, c;
while (infile >> a >> b >> c)
{
control_points.push_back(Vec(a, b, c));
}
}
void ReadTransformationPoint()
{
ifstream tranfile("E:\\ExperimentalData\\expData\\test\\mv.txt");//C:\\Users\\Administrator\\Desktop
//E:\\ExperimentalData\\expData\\test\\zhenshi700.txt
float a, b, c,N1,N2,N3,N4,N5,N6;
while (tranfile>>a>>b>>c)//tranfile >> a>> b >> c>>N1>>N2>>N3>>N4>>N5>>N6
{
TransformationPoint.push_back(Vec(a, b, c));
}
}
void reaeAllPoints()
{
//c_obj 定义一个网格对象
int mask; //定义mask
//注意your filePath不能有中文路径
vcg::tri::io::ImporterOBJ::Open(m_obj, "E:\\ExperimentalData\\expData\\test\\524.obj", mask);
//为每个点计算法线并归一化
vcg::tri::RequirePerVertexNormal(m_obj);
vcg::tri::UpdateNormal::PerVertexNormalized(m_obj);
std::vector &vs = m_obj.vert;
std::vector &es = m_obj.edge;
std::vector &fs = m_obj.face;
for (auto i = 0; i < m_obj.vert.size(); ++i)
{
MyVertex v = vs[i];
EnteredPoint.push_back(Vec(v.P().X(), v.P().Y(), v.P().Z()));
}
}
void OutputPoints()
{
MyVertex v;
for (int i = 0; i < EnteredPoint.size(); i++)
{
v.P().X() = AfterDeformPoint[i].x;
v.P().Y() = AfterDeformPoint[i].y;
v.P().Z() = AfterDeformPoint[i].z;
c_obj.vert.push_back(v);
//cout << "x= "<< AfterDeformPoint[i].x << "y= " << AfterDeformPoint[i].y << "z= " << AfterDeformPoint[i].z << endl;
}
/*for (size_t i = 0; i < c_obj.vert.size(); i++)
{
cout <<"v"<<" "<< c_obj.vert[i].P().X() << " " << c_obj.vert[i].P().Y() << " " << c_obj.vert[i].P().Z()<< endl;
}*/
c_obj.edge = m_obj.edge;
c_obj.face = m_obj.face;
//vcg::tri::BuildMeshFromCoordVectorIndexVector(c_obj, c_obj.vert, c_obj.face);
//vcg::tri::Octahedron(c_obj);
vcg::tri::io::ExporterOBJ::Save(c_obj, "C:\\Users\\Administrator\\Desktop\\c_obj.obj", 0);
}
void outDataToTxt()
{
ofstream location_out;
///*/注意路径前面不能有!空格否则会读不进去坐标//
location_out.open("E:\\ExperimentalData\\expData\\test\\location_out.txt", std::ios::out | std::ios::app); //以写入和在文件末尾添加的方式打开.txt文件,没有的话就创建该文件。
if (!location_out.is_open())
cout << "open file error" << endl;
for (int i = 0; i < EnteredPoint.size(); i++)
{
location_out << "v " << AfterDeformPoint[i].x << " " << AfterDeformPoint[i].y << " " << AfterDeformPoint[i].z << endl;
}
location_out.close();
}
int main()
{
reaeAllPoints();
ReadControlPoint();
ReadTransformationPoint();
calc_tps();
outDataToTxt();
system("pause");
return 0;
} 代码水平有限,也是自己摸索。真实点云作变形,计算出的模型顶点坐标会是特别大的数简直离谱。懂的大佬有没有知道古建筑三维变形最好用什么变形算法~难道只有拉普拉斯吗?