泛函分析 03.05 内积空间与Hilbert空间 - 可分的Hilbert空间

§3.5可分的Hilbert空间 

3.5.1线性无关组的正交化算法 

定理3.5.1设{x n }是内积空间H中的可数子集,则在 
H中存在标准正交列{e n },使得{e n }与{x n }张成的 
子空间相同. 
分析:利用Gram−Schmidt正规正交化算法找到一组标准正交列. 
证明:(1)设x n 1  是{x n }中的第一个不等于零的元素,令 
e 1 =x n 1  ∥x n 1  ∥  
(2)记M 1 =span{e 1 }=span{x n 1  }, 
设x n 2  是{x n }中第一个不属于M 1 的元,记 
h 2 =x n 2  −(x n 2  ,e 1 )e 1 ,(3.5.1) 
则h 2 ≠0,且(h 2 ,e 1 )=(x n 2  ,e 1 )−(x n 2  ,e 1 )=0, 
于是h 2 ⊥e 1 .令 
e 2 =h 2 ∥h 2 ∥ (3.5.2) 
(3)记M 2 =span{e 1 ,e 2 }=span{x n 1  ,x n 2  }. 
继续上面的做法,⋯ 
我们得到h k : 
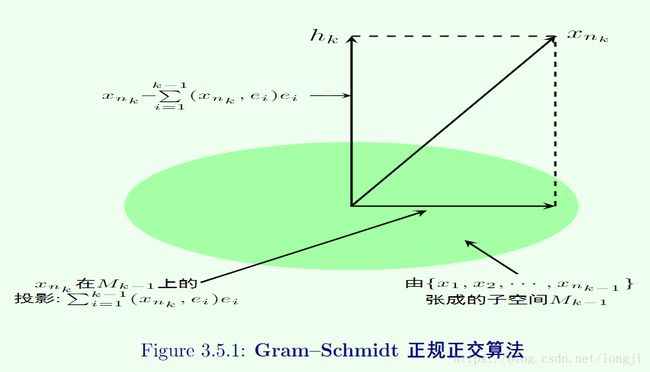
h k =x n k  −∑ i=1 k−1 (x n k  ,e i )e i (k=3,4,⋯),(3.5.3) 
则h k ≠0,且h k ⊥e i (i=1,2,⋯,k−1). 
令 
e k =h k ∥h k ∥ (3.5.4) 

(4)如果{x n }张成的子空间是有限维的,则以上做法经 
过有穷次将停止. 
若是无穷维的,则一直做下去,得到标准正交列{e n } ∞ n=1 . 
(5)由于对于每一个k,e k 可以由{x n 1  ,⋯,x n k  }线性表示, 
并且每一个{x n k  }也可用{e 1 ,⋯,e k }线性表示, 
所以{e n }与{x n }张成相同的子空间. 
注：定理中由线性无关集得到标准正交系的方法称为 
Gram−Schmidt正规正交算法(图3.5.1). 

例3.5.2Legendre多项式 
在L 2 [−1,1]空间中,考虑下列可数子集 
x 1 (t)=1,x 2 (t)=t,⋯,x n+1 (t)=t n ,⋯ 
显然它们是线性无关的,根据Gram−Schmidt正规正交算法, 
e 1 =x 1 ∥x 1 ∥ , 
h k =x k −∑ i=1 k−1 (x k ,e i )e i ,e k =h k ∥h k ∥ ,k=2,3,⋯ 
我们可以得到一个由多项式组成的正交列{e n },由正交化 
程序可知多项式e n 的次数正好是n−1,并且 
span{e n }=span{x n }. 
由于多项式的全体在L 2 [−1,1]中稠密,于是可知 
span ¯ ¯ ¯ ¯ ¯ ¯ ¯  {e n }=L 2 [−1,1], 
根据正交基的定义,多项式正交列{e n }是L 2 [−1,1]中 
的正交基. 
通过计算我们可以得到: 
e n+1 =2n+12  − − − − − −  √ P n ,n=0,1,⋯(3.5.5) 
其中 
P n =12 n n! d n dt n  [(t 2 −1) n ]. 
P n 是n阶的Legendre多项式. 
通过分部积分等计算可以直接验证: 
(P n ,P m )=0,n≠m,∥e n ∥=1, 
即它们构成L 2 [−1,1]中的一个正交列.其中 
P 0 (t)=1, 
P 1 (t)=t, 
P 2 (t)=12 (3t 2 −1), 
P 3 (t)=12 (5t 3 −3t), 
P 4 (t)=18 (35t 4 −30t+3), 
P 5 (t)=18 (63t 5 −70t 3 +15t), 

注1：可以验证Legendre多项式是Legendre方程 
(1−t 2 )P ′′ n −2tP ′ n +n(n+1)P n =0(3.5.6) 
的解. 
注2：在L 2 [a,b]空间,令 
q n =1∥p n ∥ p n ,p n (t)=P n (s),s=1+2t−bb−a , 
则{q n }是L 2 [a,b]空间的标准正交基. 

3.5.2可分的Hilbert空间与l 2 等距同构 

定理3.5.1表明一个无穷维的Hilbert空间一定包含一个标准正交列. 
问题:Hilbert空间是否一定存在标准正交基? 
当内积空间完备时,我们有 

定理3.5.3设H是一个Hilbert空间,则H是可分的, 
当且仅当H中有元素个数至多可数的标准正交基S. 
如果S中元素的个数N<∞,则H等距同构于K N  
(K是线性空间的数域); 
如果N=∞,则H等距同构于l 2 . 
证明：“⇒”从H可分来证明H中有至多可数的标准正交基. 
(i)由可分的定义,可设{x n } ∞ n=1 是H中可数稠密子集. 
则其中必存在一个线性无关的子集 
{y n } N n=1 (N<∞或N=∞,至多可数个), 
使得 
span{y n } N n=1 =span{x n } ∞ n=1 (3.5.7) 
(ii)由定理3.5.1,由{y n } N n=1 可以构造出一个标准正交列 
{e n } N n=1 ,且 
span ¯ ¯ ¯ ¯ ¯ ¯ ¯  {e n } N n=1 =span ¯ ¯ ¯ ¯ ¯ ¯ ¯  {y n } N n=1 =H(3.5.8) 
所以{e n } N n=1 是H的标准正交基. 
“⇐”由H中有至多可数的标准正交基来证明H可分. 
设{e n } N n=1 (N<∞或N=∞) 
是H中至多可数的标准正交基. 
则集合 
A={x=∑ n=1 N a n e n |Rea n 与Ima n 是有理数}(3.5.9) 
是H中的可数稠密子集. 
事实上,对于任何的y∈H和∀ε>0,因为{e n } ∞ n=1  
是H中的标准正交基,于是 
y=∑ n=1 ∞ β n e n ,其中∑ n=1 ∞ |β n | 2 <∞, 
这样存在正整数K,使得 
∑ n=K+1 ∞ |β n | 2 <ε 2 2  
对于n=1,⋯,K,我们选择实部和虚部都是有理数的α n ,使得 
|β n −α n | 2 <ε 2 2K , 
令x=∑ n=1 K α n e n ∈A,则 
∥y−x∥ 2 =∑ n=1 K |β n −α n | 2 +∑ n=K+1 ∞ |β n | 2 <ε 2 , 
这说明A在H中稠,从而H是可分的. 

对于标准正交基{e n } N n=1 (N<∞或N=∞), 
作映射 
T:x→{(x,e n )} N n=1 (∀x∈H)(3.5.10) 
容易验证T是从H到K N (当N<∞) 
或从H到l 2 (N=∞)的一对一在上的线性同构. 
根据Parseval等式,我们有 
∥x∥ 2 =∑ n=1 N |(x,e n )| 2 (∀x∈H)(3.5.11) 
另外,对∀x,y∈H, 
(x,y)=(∑ i=1 N (x,e i )e i ,∑ j=1 N (y,e j )e j ) 
=∑ i=1 N (x,e i )(y,e i ) ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯  =(Tx,Ty)(3.5.12) 
因此,T还保持内积不变(于是相应的范数也不变) 
故当N<∞时,H等距同构于K N ; 
而当N=∞(可数)时,H等距同构于l 2 . 
注1：定理表明：可分的内积空间具有至多可数的标准正交基. 
注2：定理说明, 
任何一个无穷维可分的Hilbert空间都可以表示为“坐标形式”的l 2 空间, 
即可分的内积空间中的每个元素都于一组由可数无穷有序数组 
组成的坐标一一对应.