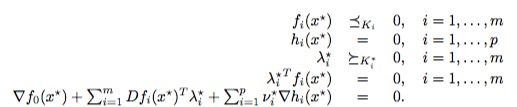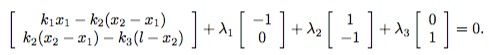Lagrange
转自:https://dubur.github.io/2015/11/24/Lagrange-Dual-Problem/
Lagrange对偶函数
我们称这个问题为原始问题(primal problem),对于这样的优化问题,相信之前学习过Lagrange乘数法的话会比较熟悉,但是与一般问题不同的是上面的问题包含不等式约束,这里我们先放一放, 首先写出目标函数L:
该函数在Convex Optimization一书中被称为Lagrangian,式中αα和ββ是Lagrange乘子(我们假设alpha大于0),显然Lagrangian函数是关于x,αα和ββ的函数
对于每一组αα,ββ,我们在f(x)f(x)的定义域上求取Lagrangian的下确界,产生的新的函数表达式如下:
那么对偶函数有什么用呢?
从定义上看,对偶函数定义了原问题所有可行解的下界,因为对于任何一个可行解x∼x∼,无论αα和ββ的值为多少,Lagrangian后面两项的和不会大于0,所以Lagrangian(x∼)Lagrangian(x∼) 的值一定小于等于f(x∼)f(x∼),而对偶函数又是Lagrangian的下确界,所以我们有:
这里p∗p∗表示原始问题的任一可行解
Lagrange对偶函数与共轭函数的关系
清楚对偶函数的定义之后,我们继续介绍共轭函数的概念,之所以需要了解这个概念的原因是因为共轭函数拥有一个非常优秀的性质:无论原函数是否是凸函数,共轭函数一定是凸函数
首先需要弄清楚共轭函数的定义:
我们可以大致猜测共轭函数的性质,由于共轭函数其实隐含着求最大值的目的,因此我们可以简单地把它看作求极值问题,那么显然对函数直接求导可以得出共轭函数在某个特定输入y处的函数值,即
得出x与y的关系x=f′−1(y)x=f′−1(y),再把上式带入到yTx−f(x)yTx−f(x)就可以求出解析式了。
由于共轭函数凹凸性的优势是的它在优化问题中非常有优势,下一步我们看共轭函数与Lagrange对偶函数的关系,假设原问题的约束条件为线性函数(SVM的函数间隔约束显然也是线性约束):
由对偶函数的定义我们有:
我们成功地从对偶问题中找到了共轭函数,因此对于仅有线性约束条件的优化问题而言对偶函数也一定是凸的
Lagrange对偶问题
我们已经知道了对偶函数的优良性质(当然约束条件要求是线性函数),如果我们能想办法将对偶函数用到原始问题的求解上,那么就能够方便地求出最后的解,因此这里我们引入对偶问题
对偶问题的数学表达如下: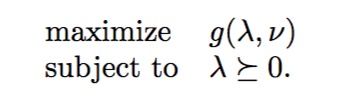 前面讲过对偶函数定义了原始问题可行解的下界,那么对偶问题的目标就是试图从找到这些下界的最大值,当然我们前面已经假设αα必须大于零。这也是为什么在许多SVM教程中对偶函数被定义为maxminL(x)maxminL(x)的原因
前面讲过对偶函数定义了原始问题可行解的下界,那么对偶问题的目标就是试图从找到这些下界的最大值,当然我们前面已经假设αα必须大于零。这也是为什么在许多SVM教程中对偶函数被定义为maxminL(x)maxminL(x)的原因
弱对偶与强对偶
由于对偶函数的保证了凹凸性,所以对偶问题的求解非常方便,我们把对偶问题的解记为d∗d∗,有我们之前的结论有:
如果我们能把不等号转变为等号,那么原始问题的解就求出来了,同时如果d\*=p\*d\*=p\*,那么弱对偶就变成了强对偶。
一般情况下强对偶的要求比较苛刻,仅在某些条件下强对偶才成立,最常见的就是Slater条件,但是Slater条件要求原问题是convex的,因此这里到了最关键的一步:利用KKT条件
KKT条件
KKT条件在convex optimizaiton中的描述如下:
We now assume that the functions f0, . . . , fm, h1, . . . , hp are differentiable (and therefore have open domains), but we make no assumptions yet about convexity.
KKT conditions for nonconvex problems
As above, let x⋆ and (λ⋆,ν⋆) be any primal and dual optimal points with zero duality gap. Since x⋆ minimizes L(x, λ⋆, ν⋆) over x, it follows that its gradient must vanish at x⋆, i.e.,dualty gap的意思是原问题解p∗p∗和对偶问题解d∗d∗的差值,显然强对偶情况下差值为0,按照Lagrange乘数法的思想,Lagrangian函数在x∗x∗处的导数为0
式中Dfi(x∗)Dfi(x∗)表示的是约束函数fifi在x∗x∗处的导数,从上式中我们可以推导出KKT条件(偷懒直接上图):
当然这里要求fifi为凸函数,hihi为线性函数(仿射)且两者均可导,函数fifi和hihi分别表示不等式约束和等式约束,前两个式子是原始问题的要求,图中λλ和υυ对应前面的αα和ββ,我们关注第三和第四个式子,结合SVM我们可以发现如果Lagrange乘子λλ大于0,那么对应的不等约束变为等式约束,对应支持向量的情况,如果λλ等于0,那么对fifi的值没有要求,对应非支持向量的情况。
同时KKT条件也说明了我们为什么在前面定义Lagrangian时要求αα大于等于0的原因。
笔者在看其他教程时一直不明白第三第四个式子从哪里推导出来的,书中好像没有给出严密的证明和推导,但是给出了一种非常直观的interpretation——物理学中的弹簧问题
简单而言就是两个滑块由三个弹簧链接,并且位于两堵墙中间,求平衡状态下使整个系统的能量最小的x1x1,x2x2 首先求能量函数为:
从图中我们可以看出一些基本的约束条件(两堵墙中间要有足够的空间,滑块之间不能重叠): w2−x1≤0w2−x1≤0, w+x1+x2w+x1+x2, w2−l+x2≤0w2−l+x2≤0
因此我们得到了原始的优化问题,假设Lagrange乘子分别为λ1λ1,λ2λ2,λ3λ3,那么由KKT条件我们有(对应第三第四个式子)
λi≥0λi≥0
且λ1(w/2−x1)=0λ1(w/2−x1)=0, λ2(w−x2+x1)=0λ2(w−x2+x1)=0, λ3(w/2−l+x2)=0λ3(w/2−l+x2)=0
同时由于在解的位置梯度为0,我们有:
另一方面,由于系统处于平衡状态,滑块一定是受力平衡的,我们对滑块进行受力分析:
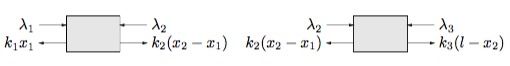 动手写一下受力平衡方程就可以发现与上面的梯度为0的式子是一样的,说明了Lagrange乘子可以看作是题目中滑块受到的反作用力,KKT条件与平衡状态的受力分析殊途同归
动手写一下受力平衡方程就可以发现与上面的梯度为0的式子是一样的,说明了Lagrange乘子可以看作是题目中滑块受到的反作用力,KKT条件与平衡状态的受力分析殊途同归
这个例子说明了KKT条件是对于原始问题另一角度的解读,如果我们的优化问题存在一个“平衡状态”的话,那么我们可以通过解对偶问题来获得原始问题的解
推广到SVM,如果支持向量确定的话那么相当于给出了“平衡状态”,我们可以直接求解对偶问题来求分割超平面,而当我们获得训练集的时候其实支持向量已经确定了(当然可能需要核函数映射)。