Circles Inside a Square(几何题)
题目描述
You have 8 circles of equal size and you want to pack them inside a square. You want to minimize the size of the square. The following figure illustrates the minimum way of packing 8 circles inside a square:
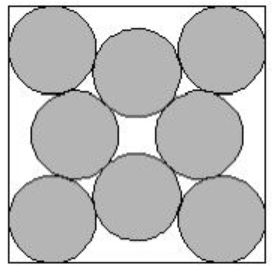
Given the radius, r, find the area of the minimum square into which 8 circles of that radius can be packed.
输入
There is one input line, it consists of a positive real number (between 0.001 and 1000, inclusive) denoting the radius, r.
输出
Print the area of the minimum square where 8 circles of radius r can be packed. Print 5 digits after the decimal. Your output is considered correct if it is within ±0.00001 of the judge’s output.
样例输入
0.1
样例输出
0.34383
题意:
将八个圆放到一个正方形中,给出圆的半径求出正方形的面积
相信很多人都会去推公式小声说我也去推了公式 ,后来采用了偷工减料的方法,根据给出的数据推出可能会成立的结论,没想到还真过了[手动滑稽]
#pragma GCC optimize("Ofast,unroll-loops,no-stack-protector,fast-math")
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#pragma GCC optimize (2)
#pragma G++ optimize (2)
#include 解释一下这里的1.8367的来源:
r==0.1时的结果0.34383进行开方,减去四倍的半径就是0.18637然后目前得到的这个数就是比较难球求的中间部分的长度,它必然和半径有关,而且这个关系肯定是成特定比例的因此呢,中间难求的部分和2r的关系通过这个关系来解决0.18637/(2r)等于1.8637
上面给出的代码有测试输出
2020.7.25更
代码正解:
#include