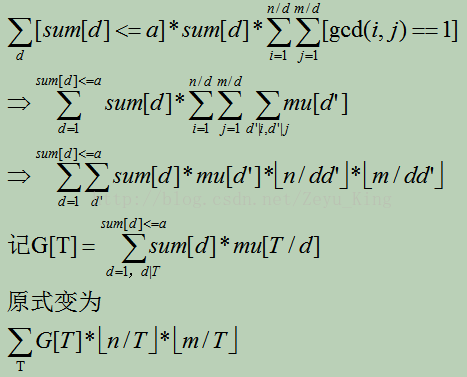欧拉函数&莫比乌斯反演
近几天做了几道有关反演的问题,在此集合一下吧。
1、[BZOJ 2301]HAOI2011 Problem b
2、[BZOJ 2440]中山市选2011 完全平方数
3、gcd
4、[BZOJ 2186]SDOI2008 莎拉公主的困惑
5、[BZOJ 3529]SDOI2014 数表
(蒟蒻自认为反演一类的的题目重要的就是记住两个重要的公式:1、sigma(mu[i] , i|n ) = [n==1] 2、sigma(phi[i] , i|n ) = n)
题解:
1、[BZOJ 2301]HAOI2011 Problem b
这基本上算是入门题了吧。。。。
gcd(a,b)==k等价于gcd(a/k,b/k)==1,这样我们将范围除k,等价到求区间内互质的二元组数。
假设query(n,m)得到gcd(a,b)==1的数量,那么答案很明显就是gcd(b,d) - gcd(a-1,d) - gcd(b,c-1) + gcd(a-1,c-1)
简单了,下面简述一下推导过程吧
为了不被多组数据卡掉,我们观察到n/k的答案只有不超过根号n个不同答案,对mu[]前缀和优化,那么每次询问时O(sqrt(n))的复杂度
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int l,r,ans,mid,INF,K,Case,tot;
int prime[41005],mu[41005],i,j;
bool check[41005];
void init(){
mu[1]=1;
for (i=2;i<41000;i++){
if (!check[i]) mu[i]=-1, prime[++tot]=i;
for (j=1;j<=tot;j++){
if (i*prime[j]>41000) break;
check[i*prime[j]]=1;
if (i%prime[j]==0) {mu[i*prime[j]]=0;break;}
else mu[i*prime[j]] = -mu[i];
}
}
}
bool Judge(){
int ret=0;
for (int i=1;i*i<=mid;i++)
ret+=(mid/i/i)*mu[i];
return (ret>=K);
}
int main(){
//freopen("2440.in","r",stdin);
//freopen("2440.out","w",stdout);
init();
INF=41000; INF=INF*INF;
scanf("%d",&Case);
while (Case--){
scanf("%d",&K);
l=1; r=INF;
while (l<=r){
mid=((long long)l+r)>>1;
if (Judge()) ans=mid, r=mid-1;
else l=mid+1;
}
printf("%d\n",ans);
}
return 0;
}
2、[BZOJ 2440]中山市选2011 完全平方数
好题啊~~~~~~
首先必须想到一个利器——二分!
我们二分出一个数怎样检验有多少个完全平方数比他小呢?
从莫比乌斯函数的定义来看
接下来利用容斥从n中减去为平方数倍数的数。
如果一个数有平方因子,莫比乌斯函数值为0,不必考虑。
如果不为0,实质上就是容斥,减去mu[i]*n/(i*i)即可
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int l,r,ans,mid,INF,K,Case,tot;
int prime[41005],mu[41005],i,j;
bool check[41005];
void init(){
mu[1]=1;
for (i=2;i<41000;i++){
if (!check[i]) mu[i]=-1, prime[++tot]=i;
for (j=1;j<=tot;j++){
if (i*prime[j]>41000) break;
check[i*prime[j]]=1;
if (i%prime[j]==0) {mu[i*prime[j]]=0;break;}
else mu[i*prime[j]] = -mu[i];
}
}
}
bool Judge(){
int ret=0;
for (int i=1;i*i<=mid;i++)
ret+=(mid/i/i)*mu[i];
return (ret>=K);
}
int main(){
//freopen("2440.in","r",stdin);
//freopen("2440.out","w",stdout);
init();
INF=41000; INF=INF*INF;
scanf("%d",&Case);
while (Case--){
scanf("%d",&K);
l=1; r=INF;
while (l<=r){
mid=((long long)l+r)>>1;
if (Judge()) ans=mid, r=mid-1;
else l=mid+1;
}
printf("%d\n",ans);
}
return 0;
}
3、gcd
(由于网上没找到原题,就简述一下题意吧)
给你n个正整数,以及一个正整数k。然后有q个询问,每次询问一个x。要求回答从这n个数中选出正好k个数并且使得他们的最大公约数是x的方案数是多少。输出答案mod 10^9+7值。n,q,x<=10^6,k<=n。时限:5s
还是容斥。。。。。
sum[]记录数字i的约数有多少个,这样方便计算。
预处理计算对于每一个x的答案ans[x],用到组合之类的东西。
复杂度大约是nlogn。
询问直接输了,具体还是见代码吧。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int Maxn=1000001, Mod=(1e9)+7;;
#define C(n,m) ((LL)jc[n]*ny[m]%Mod*ny[(n)-(m)]%Mod)
int check[Maxn],jc[Maxn],ny[Maxn],mu[Maxn],prime[Maxn];
int sum[Maxn],i,j,tot,x,n,k,Case;
LL ans[Maxn];
int qck(int a,int b){
int ret=1;
for (;b>0;b>>=1){
if (b&1) ret=(LL)ret*a%Mod;
a=(LL)a*a%Mod;
}
return ret;
}
void init(){
mu[1]=1;
for (i=2;i<Maxn;i++){
if (check[i]==0) { mu[i]=-1;prime[++tot]=i; }
for (j=1;j<=tot;j++){
if (prime[j]*i>=Maxn) break;
check[prime[j]*i]=prime[j];
if (i%prime[j]) mu[prime[j]*i]=-mu[i];
else { mu[prime[j]*i]=0;break; }
}
if (check[i]==0) ny[i]=qck(i,Mod-2);
else ny[i]=(LL)ny[i/check[i]]*ny[check[i]]%Mod;
}
jc[0]=ny[0]=1;
jc[1]=ny[1]=1;
for (i=2;i<Maxn;i++){
jc[i]=(LL)jc[i-1]*i%Mod;
ny[i]=(LL)ny[i]*ny[i-1]%Mod;
}
}
int main(){
freopen("gcd.in","r",stdin);
freopen("gcd.out","w",stdout);
init();
scanf("%d%d",&n,&k);
for (i=1;i<=n;i++){
scanf("%d",&x);
sum[x]++;
}
for (i=1;i<Maxn;i++)
for (j=i+i;j<Maxn;j+=i)
sum[i]=sum[j]+sum[i];
for (i=1;i<Maxn;i++)
for (j=1;i*j<Maxn;j++){
if (sum[i*j]<k) continue;
ans[i]=(ans[i]+(LL)mu[j]*C(sum[i*j],k)+Mod)%Mod;
}
scanf("%d",&Case);
while (Case--){
scanf("%d",&x);
printf("%I64d\n",ans[x]);
}
return 0;
}
鸣谢zy给我的启发!
如果0<x<n,x与n互质,那么x+n也一定与n互质。
否命题也成立。
那么我们只有求出在m!中与m!互质的数,也就是phi(m!)。
答案就是n!/m!*phi(m!)。
关于计算答案我用了些什么线性逆元乱七八糟的东西,理论上复杂度还可以,实际上被卡常数了,跑得很慢的。
trick:虽然题目上没说,但是数据上是这么给的:R是一个比较大的质数(大于所有n,m)
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int Maxn=10000001;
int Case,Mod,check[Maxn],prime[Maxn],tot,i,j;
int phi[Maxn],jc[Maxn],ny[Maxn],n,m,l,r,mid,t,ans;
int qck(int a,int b){
int ret=1;
for (;b>0;b>>=1){
if (b&1) ret=(LL)ret*a%Mod;
a=(LL)a*a%Mod;
}
return ret;
}
void init(){
jc[0]=1; ny[0]=1;
jc[1]=1; ny[1]=1;
for (i=2;i<Maxn;i++){
if (check[i]==0) prime[++tot]=i;
for (j=1;j<=tot;j++){
if (i*prime[j]>=Maxn) break;
check[i*prime[j]]=prime[j];
if (i%prime[j]==0) break;
}
jc[i]=(LL)jc[i-1]*i%Mod;
if (check[i]==0) ny[i]=qck(i,Mod-2);
else ny[i]=(LL)ny[check[i]]*ny[i/check[i]]%Mod;
}
for (i=1,phi[0]=1;i<=tot;i++)
phi[i]=(LL)phi[i-1]*(prime[i]-1)%Mod*ny[prime[i]]%Mod;
for (i=1;i<Maxn;i++)
ny[i]=(LL)ny[i-1]*ny[i]%Mod;
}
int main(){
//freopen("2186.in","r",stdin);
//freopen("2186.out","w",stdout);
scanf("%d%d",&Case,&Mod);
init();
while (Case--){
scanf("%d%d",&n,&m);
if (m>n) {printf("0\n");continue;}
l=1; r=tot; t=0;
while (l<=r){
mid=(l+r)>>1;
if (prime[mid]<=m) t=mid, l=mid+1;
else r=mid-1;
}
ans=(LL)jc[m]*phi[t]%Mod*jc[n]%Mod*ny[m]%Mod;
printf("%d\n",ans);
}
return 0;
}
5、[BZOJ 3529]SDOI2014 数表
(终于到最后一题了![]() )
)
其实题目里把a给很大是无用的,算一下表格内最大的数字不会超过50W
以sum[]为关键字排序,逐步更新G[],用Problem b的方法分段优化时间,用树状数组维护G[],复杂度大约就是O( q*logn*sqrt(n) )
贴上丑丑的代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lowbit(x) ((x)&(-(x)))
int ans[20005],tr[100005],prime[100005];
int i,j,k,kk,N,tot,mu[100005];
bool check[100005];
struct query
{
int n,m,k,num;
bool operator <(const query &a)const
{ return k<a.k; }
} q[20005];
struct divsum
{
int x,y;
bool operator <(const divsum &a)const
{ return y<a.y; }
}sum[100005];
void init(){
for (i=1;i<=100000;i++){
for (j=1;j*j<=i;j++)
if (i%j==0){
sum[i].y+=j;
if (i/j!=j) sum[i].y+=i/j;
}
sum[i].x=i;
}
sort(sum+1,sum+100001);
mu[1]=1;
for (i=2;i<=100000;i++){
if (check[i]==0) {prime[++tot]=i;mu[i]=-1;}
for (j=1;j<=tot;j++){
if (prime[j]*i>100000) break;
check[prime[j]*i]=1;
if (i%prime[j]==0) {mu[i*prime[j]]=0;break;}
else mu[i*prime[j]]=-mu[i];
}
}
}
void ins(int x,int y){
for (int i=x;i<=100000;i+=lowbit(i))
tr[i]+=y;
}
int get(int x){
int ret=0;
for (int i=x;i>0;i-=lowbit(i))
ret+=tr[i];
return ret;
}
int get(int l,int r)
{ return get(r)-get(l-1);}
int main(){
//freopen("table.in","r",stdin);
//freopen("table.out","w",stdout);
init();
scanf("%d",&N);
for (i=1;i<=N;i++){
scanf("%d%d%d",&q[i].n,&q[i].m,&q[i].k);
q[i].num=i;
}
sort(q+1,q+N+1);
for (i=1,j=1;i<=N;i++){
for (;j<=100000 && sum[j].y<=q[i].k;j++)
for (k=1;k*sum[j].x<=100000;k++)
ins(k*sum[j].x,sum[j].y*mu[k]);
for (k=1;k<=q[i].n&&k<=q[i].m;k=kk+1){
kk=min( q[i].n/(q[i].n/k), q[i].m/(q[i].m/k) );
ans[q[i].num]+=get(k,kk)*(q[i].n/k)*(q[i].m/k);
}
if (ans[q[i].num]<0){
ans[q[i].num]+=2147483647;
ans[q[i].num]++;
}
}
for (i=1;i<=N;i++)
printf("%d\n",ans[i]);
return 0;
}
——————————————————————————————————————————
最后戳两个题目,以后做吧:
[bzoj 2154]Crash的数字表格
[bzoj 3434]wc2014时空穿梭