四元数&MPU9250

四元数

四元数可以理解为定义一个要做的旋转，旋转轴为 V=(Vx,Vy,Vz) ,旋转角度为 θ (右手法则的旋转)。
q=[q0,q1,q2,q3]
q=[cos(θ2),sin(θ2)i,sin(θ2)j,sin(θ2)k]

四元数性质

i2=j2=k2=ijk=−1
jk=i
ki=j
ij=k
kj=−i
ik=−j
ji=−k
只有单位四元数才可以表示旋转,单位化四元数：
normal = q02+q12+q22+q32−−−−−−−−−−−−−−−−−√
q0/=normal
q1/=normal
q2/=normal
q3/=normal

四元数欧拉角相互转换

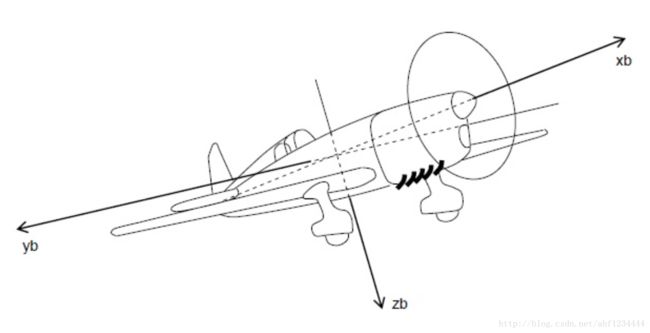
轴公约：
1. 绕xb轴旋转机体得到横滚角 φ
2. 绕yb轴旋转机体得到俯仰角 θ
3. 绕zb轴旋转机体得到偏航角 ψ

四元数转欧拉角

⎡⎣⎢φ(横滚角)θ(俯仰角)ψ(偏航角)⎤⎦⎥=⎡⎣⎢atan2(2(q0q3+q1q2),1−2(q32+q12))arcsin(2(q0q1−q2q3))atan2(2(q0q2+q3q1),1−2(q12+q22))⎤⎦⎥

欧拉角转四元数

⎡⎣⎢⎢⎢q0q1q2q3⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢cos(φ2)cos(θ2)cos(ψ2)+sin(φ2)sin(θ2)sin(ψ2)cos(φ2)sin(θ2)cos(ψ2)+sin(φ2)cos(θ2)sin(ψ2)cos(φ2)cos(θ2)sin(ψ2)−sin(φ2)sin(θ2)cos(ψ2)sin(φ2)cos(θ2)cos(ψ2)−cos(φ2)sin(θ2)sin(ψ2)⎤⎦⎥⎥⎥⎥⎥⎥

加速计

从加速计读出的数据为机体坐标系下的三轴加速度
对机体坐标系下的三轴加速度进行单位化
normal=ax2+ay2+az2−−−−−−−−−−−−−√
ax=ax/normal
ay=ay/normal
az=az/normal
在世界坐标系下的重力向量为 ⎡⎣⎢001⎤⎦⎥ 转换到机体坐标系下需要通过旋转矩阵来求得
⎡⎣⎢vxvyvz⎤⎦⎥=C×⎡⎣⎢001⎤⎦⎥
C 是方向余弦矩阵

C=⎡⎣⎢⎢q02+q12−q22−q322∗(q1q2+q0q3)2∗(q1q3−q0q2)2∗(q1q2−q0q3)q02−q12+q22−q322∗(q2q3+q0q1)2∗(q1q3+q0q2)2∗(q2q3−q0q1)q02−q12−q22+q32⎤⎦⎥⎥

如果想从机体坐标转换到世界坐标则旋转矩阵C变为C的逆即可(已证
明旋转矩阵的逆矩阵与旋转矩阵的转置矩阵 CT 是相等的)
理论上 ⎡⎣⎢vxvyvz⎤⎦⎥ 应该等于重力向量 ⎡⎣⎢001⎤⎦⎥ 但是由于四元数主要由陀螺仪计算，由于陀螺仪积分存在漂移所以实际上这两个向量不相等。这时候我们就可以利用向量叉乘来计算这两个向量的误差向量

E=⎡⎣⎢exeyez⎤⎦⎥=⎡⎣⎢ay∗vz−az∗vyaz∗vx−ax∗vzax∗vy−ay∗vx⎤⎦⎥

这个误差向量的物理意义是 叉乘等于|A| * |B| * sin(θ) ，由于加速计测量的向量和重力向量都是单位向量所以误差向量大小只与角度有关。
这个误差向量可以用来对陀螺仪的漂移进行修正。

陀螺仪

陀螺仪的输出数据就是机体坐标下三轴的角速度gx、gy、gz，通过三轴的角速度求得我们需要的姿态就需要用到四元数微分方程
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT
q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT
q2 = q2 + (q0*gy - q2*gz + q3*gx)*halfT
q3 = q3 + (q0*gz + q2*gy - q3*gx)*halfT
halfT为测量周期的一半

磁力计

由于加速计无法感知Z轴上的旋转运动，所以还需要用磁力计来进一步修正陀螺仪的漂移。
我们知道加速度计在静止时测量的是重力加速度，是有大小和方向的；同理，地磁计同样测量的是地球磁场的大小和方向，只不过这个方向不再是竖直向下，而是与x轴（或者y轴）呈一个角度，与z轴呈一个角度。记作 ⎡⎣⎢bxbybz⎤⎦⎥ ，这里我们让x轴对准北，所以by=0，即 ⎡⎣⎢bx0bz⎤⎦⎥ 。倘若我们知道bx和bz的精确值，那么我们就可以采用和加速度计一样的修正方法来修正。只不过在加速度计中，我们在世界坐标系中的参考向量是 ⎡⎣⎢001⎤⎦⎥ ，变成了地磁计的 ⎡⎣⎢bx0bz⎤⎦⎥ 。如果我们知道bx和bz的精确值，那么我们就可以摆脱掉加速度计的补偿，直接用地磁计和陀螺仪进行姿态解算，但是你看过谁只有陀螺仪和地磁计进行姿态解算吗？没有，因为没人会去测量当地的地磁场相对于东北天坐标的夹角，也就是bx和bz。
我们把磁力计测量的机体坐标下的三轴的磁力 ⎡⎣⎢mxmymz⎤⎦⎥ 变换到世界坐标后得到 ⎡⎣⎢hxhyhz⎤⎦⎥ 。
在世界坐标XOY平面上， ⎡⎣⎢bx0bz⎤⎦⎥ 的投影为 bx2 ， ⎡⎣⎢hxhyhz⎤⎦⎥ 的投影为 hx2+hy2 。显然，地磁计在XOY平面上的向量的大小必定相同，所以有 bx2=hx2+hy2 。而对于bz的处理，我们不做变动，令bz=hz即可。
经过这样处理之后把我们得到的 ⎡⎣⎢bx0bz⎤⎦⎥ 变换回机体坐标下得到 ⎡⎣⎢wxwywz⎤⎦⎥ 这个值再与磁力计输出 ⎡⎣⎢mxmymz⎤⎦⎥ 做向量积求误差，这样就完成了一次磁力计的修正。