梯度、散度、旋度与麦克斯韦方程组
麦克斯韦方程组在大学物理是比较难以理解的一组方程。它们的推导过程与梯度、散度、与旋度具有密切的关系。本文主要通过对三维空间中梯度、散度与旋度的解释来分析麦克斯韦方程组。为了方便表示,这里 f ( x , y , z ) f(x,y,z) f(x,y,z)表示一个含有三个变量x,y,z的一个函数,并且设 f ( x , y , z ) = x 2 + y 2 + z 2 f(x,y,z)=x^2+y^2+z^2 f(x,y,z)=x2+y2+z2。 F ⃗ = < P , Q , R > \vec{F}=<P,Q,R> F=<P,Q,R>表示空间中的矢量场。可以是梯度场、速度场、力场等。这里就假设是函数f(x,y,z)对应的梯度场。
0. ▽ \triangledown ▽ 算子
又叫“del”算子,即 < ∂ ∂ x , ∂ ∂ y , ∂ ∂ z > <\frac{\partial}{\partial x}, \frac{\partial}{\partial y},\frac{\partial}{\partial z}> <∂x∂,∂y∂,∂z∂>。可以理解为一个符号向量,向量里的元素是偏微分运算符号,没有任何具体意义,只是一个表示方法。
1. 梯度、散度、旋度
有了 ▽ \triangledown ▽算子,梯度、散度、旋度都可以用 ▽ \triangledown ▽向量来表示。
梯度 gradient
函数 f ( x , y , z ) f(x,y,z) f(x,y,z)(标量)的梯度可以理解为 ▽ \triangledown ▽向量与函数的乘积,即:
g r a d ( f ) = ▽ f = < ∂ ∂ x , ∂ ∂ y , ∂ ∂ z > f = < ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z > grad(f)=\triangledown f= <\frac{\partial}{\partial x},\frac{\partial}{\partial y}, \frac{\partial}{\partial z}>f=<\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}> grad(f)=▽f=<∂x∂,∂y∂,∂z∂>f=<∂x∂f,∂y∂f,∂z∂f>
针对一开始给出的例子,可知: ▽ f = < 2 x , 2 y , 2 z > \triangledown f=<2x,2y,2z> ▽f=<2x,2y,2z>
散度 divergence
散度是表示矢量扩散程度的一个量,是对场的一个运算。散度可以表示为 ▽ \triangledown ▽向量与矢量场的点积,这里以 F ⃗ = < P , Q , R > \vec{F}=<P,Q,R> F=<P,Q,R>为例子,则:
d i v ( F ⃗ ) = ▽ ⋅ F ⃗ = < ∂ ∂ x , ∂ ∂ y , ∂ ∂ z > ⋅ < P , Q , R > = ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z div(\vec{F})=\triangledown\cdot\vec{F}=<\frac{\partial}{\partial x},\frac{\partial}{\partial y}, \frac{\partial}{\partial z}>\cdot<P, Q, R>=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+ \frac{\partial R}{\partial z} div(F)=▽⋅F=<∂x∂,∂y∂,∂z∂>⋅<P,Q,R>=∂x∂P+∂y∂Q+∂z∂R
假如 F ⃗ \vec{F} F刚好是f(x,y,z)对应的梯度场,即 F ⃗ = < 2 x , 2 y , 2 z > \vec{F}=<2x,2y,2z> F=<2x,2y,2z>则:
d i v ( F ⃗ ) = 2 + 2 + 2 = 6 div(\vec{F})=2+2+2=6 div(F)=2+2+2=6
旋度 curl
旋度表示矢量场的选择程度和方向的一个矢量。可以表示为 ▽ \triangledown ▽向量与矢量场的叉积。即:
c u r l ( F ⃗ ) = ▽ × F ⃗ = ∣ i ^ j ^ k ^ ∂ ∂ x ∂ ∂ x ∂ ∂ z P Q R ∣ = < R y − Q z , P z − R x , Q x − P y > curl(\vec{F})=\triangledown\times\vec{F}=\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial x} & \frac{\partial}{\partial z} \\ P & Q & R\end{vmatrix}=<R_{y}-Q_{z}, P_{z}-R_{x}, Q_{x}-P_{y}> curl(F)=▽×F=∣∣∣∣∣∣i^∂x∂Pj^∂x∂Qk^∂z∂R∣∣∣∣∣∣=<Ry−Qz,Pz−Rx,Qx−Py>
假如此处 F ⃗ = ▽ f \vec{F}=\triangledown f F=▽f, 则:
c u r l ( F ⃗ ) = 0 curl (\vec{F})=0 curl(F)=0
推论:假如 F ⃗ \vec{F} F是梯度,则 c u r l F ⃗ curl{\vec{F}} curlF=0
2. Gauss-Green 定理与Stokes 定理
线积分
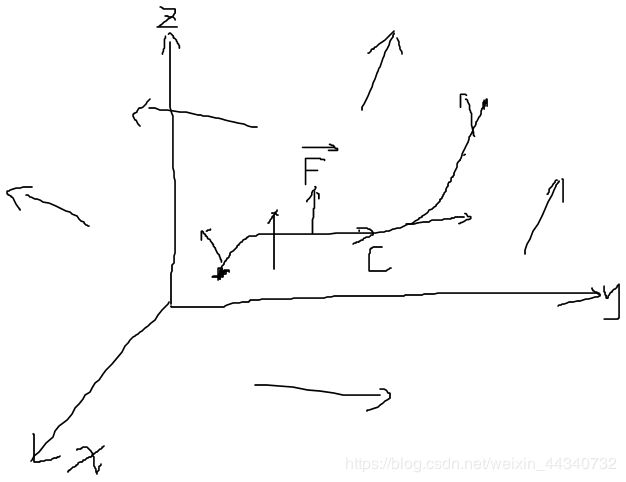
上图中, F ⃗ \vec{F} F是空间中的矢量场, C是含有方向的线段。则 F ⃗ \vec{F} F对C的积分(理解为物理上的功)可以表示为:
∫ C F ⃗ d r ⃗ = ∫ C P d x + Q d y + R d z \int_{C}\vec{F}d\vec{r}=\int_{C}Pdx+Qdy+Rdz ∫CFdr=∫CPdx+Qdy+Rdz
面积分
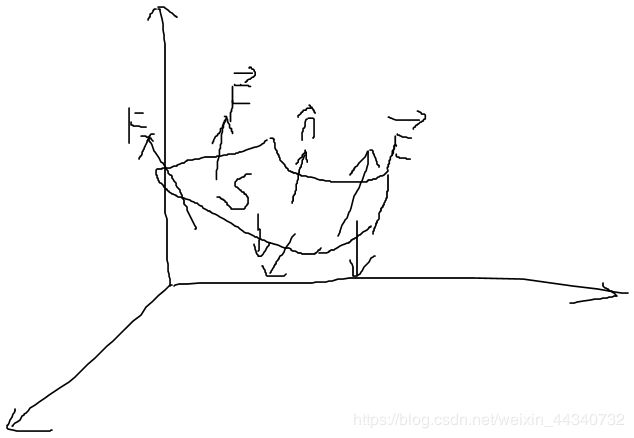
上图中,S表示空间中一个曲面, n ^ \hat{n} n^表示曲面的法向量(两个方向中选一个)。则矢量 F ⃗ \vec{F} F对曲面S的积分表示通量(Flux),即:
F l u x = ∬ S F ⃗ ⋅ n ^ d S Flux=\iint_{S}\vec{F}\cdot\hat{n}dS Flux=∬SF⋅n^dS
Gauss-Green 定理

如果S是空间中的封闭曲面,包裹了一个区域D,法向量 n ^ \hat{n} n^向外, F ⃗ \vec{F} F在D的每一个区域都定义且可微,则下式成立:
∯ S F ⃗ ⋅ d S ⃗ = ∭ D d i v ( F ⃗ ) d V \oiint_S\vec{F}\cdot d\vec{S}=\iiint_Ddiv(\vec{F})dV ∬SF⋅dS=∭Ddiv(F)dV
因此,Gauss-Green定理又叫散度定理。
Stokes 定理

如果C是一个封闭曲线,S是以C为边的任意曲面, F ⃗ \vec{F} F在S上有定义, n ^ \hat{n} n^为满足右手定则方向向外,则有如下公式:
∮ C F ⃗ ⋅ d r ⃗ = ∬ S c u r l ( F ⃗ ) ⋅ n ^ d S \oint_C\vec{F}\cdot d\vec{r}=\iint_Scurl(\vec{F})\cdot \hat{n}dS ∮CF⋅dr=∬Scurl(F)⋅n^dS
即:
∮ C F ⃗ ⋅ d r ⃗ = ∬ S ( ▽ × F ⃗ ) ⋅ n ^ d S \oint_C\vec{F}\cdot d\vec{r}=\iint_S(\triangledown\times\vec{F})\cdot \hat{n}dS ∮CF⋅dr=∬S(▽×F)⋅n^dS
推论:如果 F ⃗ \vec{F} F是梯度场,则线积分是路径无关的。

例如,在上图中,
∫ C 1 F ⃗ ⋅ d r ⃗ − ∫ C 2 F ⃗ ⋅ d r ⃗ = ∯ C : C = C 1 − C 2 F ⃗ ⋅ d r ⃗ = s t o k e s ∬ S c u r l ( F ⃗ ) ⋅ d S ⃗ \int_{C1}\vec{F}\cdot d\vec{r}-\int_{C2}\vec{F}\cdot d\vec{r}=\oiint\limits_{C:C=C1-C2}\vec{F}\cdot d\vec{r} \xlongequal{stokes}\iint_Scurl(\vec{F})\cdot d\vec{S} ∫C1F⋅dr−∫C2F⋅dr=C:C=C1−C2∬F⋅drstokes∬Scurl(F)⋅dS
因为梯度场中的curl=0,所以上式为0,即 ∫ C 1 F ⃗ ⋅ d r ⃗ = ∫ C 2 F ⃗ ⋅ d r ⃗ \int_{C1}\vec{F}\cdot d\vec{r}=\int_{C2}\vec{F}\cdot d\vec{r} ∫C1F⋅dr=∫C2F⋅dr
3. 麦克斯韦方程组

有了上述知识,麦克斯韦方程组就更容易理解。就是Gauss-Green定理和Stokes定理的运用。想要了解的更详细,请参考MIT关于多变量微积分和物理的公开课。